[题目]如图.△ABC中.D是BC上的一点.若AB=10.BD=6.AD=8.AC=17.求△ABC的面积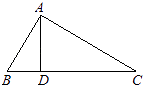．题目和参考答案——青夏教育精英家教网—

【题目】如图，△ABC中，D是BC上的一点，若AB=10，BD=6，AD=8，AC=17，求△ABC的面积．

【答案】解：∵BD2+AD2=62+82=102=AB2 ， ∴△ABD是直角三角形，
∴AD⊥BC，
在Rt△ACD中，，
∴S△ABC= ，
因此△ABC的面积为84．
答：△ABC的面积是84
【解析】根据AB=10，BD=6，AD=8，利用勾股定理的逆定理求证△ABD是直角三角形，再利用勾股定理求出CD的长，然后利用三角形面积公式即可得出答案．
【考点精析】利用勾股定理的概念和勾股定理的逆定理对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】根据下列条件，能作出平行四边形的是（　　）

A. 两组对边的长分别是3和5

B. 相邻两边的长分别是3和5，且一条对角线长为9

C. 一边的长为7，两条对角线的长分别为6和8

D. 一边的长为7，两条对角线的长分别为6和5

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知反比例函数y=﹣ ，则有
①它的图象在一、三象限：
②点（﹣2，4）在它的图象上；
③当l＜x＜2时，y的取值范围是﹣8＜y＜﹣4；
④若该函数的图象上有两个点A （x1 ， y1），B（x2 ， y2），那么当x1＜x2时，y1＜y2
以上叙述正确的是

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某课题组为了解全市九年级学生对数学知识的掌握情况，在一次数学检测中，从全市24000名九年级考生中随机抽取部分学生的数学成绩进行调查，并将调查结果绘制成如下图表：

分数段	频数	频率
x＜60	20	0.10
60≤x＜70	28	0.14
70≤x＜80	54	0.27
80≤x＜90	a	0.20
90≤x＜100	24	0.12
100≤x＜110	18	b
110≤x＜120	16	0.08

请根据以上图表提供的信息，解答下列问题：
（1）表中a和b所表示的数分别为多少；
（2）请在图中，补全频数分布直方图；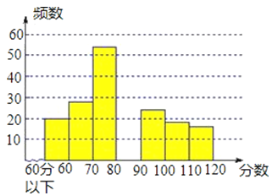

（3）如果把成绩在90分以上（含90分）定为优秀，那么该市24000名九年级考生数学成绩为优秀的学生约有多少名？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，抛物线y＝－x2＋2x＋m＋1交x轴于点A(a，0)和B（b，0），交y轴于点C，抛物线的顶点为D，下列四个判断：①当x>0时，y>0；②若a＝－1，则b＝4；③抛物线上有两点P（x1，y1）和Q（x2，y2），若x1<1< x2，且x1＋x2>2，则y1> y2；④点C关于抛物线对称轴的对称点为E，点G，F分别在x轴和y轴上，当m＝2时，四边形EDFG周长的最小值为．其中正确判断的序号是（）