
ЁОЬтФПЁПОХЃЈ1ЃЉАрЭЌбЇЮЊСЫНт 2011 ФъФГаЁЧјМвЭЅдТОљгУЫЎЧщПіЃЌЫцЛњЕїВщСЫИУаЁЧјВПЗжМвЭЅЃЌВЂНЋЕїВщЪ§ОнНјааШчЯТећРэЃЎЧыНтД№вдЯТЮЪЬтЃК

![]()

(1) АбЩЯУцЕФЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
(2) ЧѓдТОљгУЫЎСПВЛГЌЙ§ ![]() ЕФМвЭЅЪ§еМБЛЕїВщМвЭЅзмЪ§ЕФАйЗжБШЃЛ
ЕФМвЭЅЪ§еМБЛЕїВщМвЭЅзмЪ§ЕФАйЗжБШЃЛ
(3) ШєИУаЁЧјга ![]() ЛЇМвЭЅЃЌИљОнЕїВщЪ§ОнЙРМЦЃЌИУаЁЧјдТОљгУЫЎСПГЌЙ§
ЛЇМвЭЅЃЌИљОнЕїВщЪ§ОнЙРМЦЃЌИУаЁЧјдТОљгУЫЎСПГЌЙ§ ![]() ЕФМвЭЅДѓдМгаЖрЩйЛЇ ЃП
ЕФМвЭЅДѓдМгаЖрЩйЛЇ ЃП
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛ(2)дТОљгУЫЎСПВЛГЌЙ§ ![]() ЕФМвЭЅЪ§еМБЛЕїВщЕФМвЭЅзмЪ§ЕФ
ЕФМвЭЅЪ§еМБЛЕїВщЕФМвЭЅзмЪ§ЕФ ![]() ЃЛ(3)ИУаЁЧјдТОљгУЫЎСПГЌЙ§
ЃЛ(3)ИУаЁЧјдТОљгУЫЎСПГЌЙ§ ![]() ЕФМвЭЅДѓдМга
ЕФМвЭЅДѓдМга ![]() ЛЇЃЎ
ЛЇЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОндТгУЕчСПЪЧ![]() ЕФЛЇЪ§ЪЧ6ЃЌЖдгІЕФЦЕТЪЪЧ0.12ЃЌЧѓГіЕїВщЕФзмЛЇЪ§ЃЌШЛКѓРћгУзмЛЇЪ§ГЫвдЦЕТЪОЭЪЧЦЕЪ§ЃЌЦЕЪ§Г§вдзмЪ§ОЭЪЧЦЕТЪЃЌМДПЩЕУГіД№АИЃЛдйИљОнЧѓГіЕФЦЕЪ§ЃЌМДПЩВЙШЋЭГМЦЭМЃЛ
ЕФЛЇЪ§ЪЧ6ЃЌЖдгІЕФЦЕТЪЪЧ0.12ЃЌЧѓГіЕїВщЕФзмЛЇЪ§ЃЌШЛКѓРћгУзмЛЇЪ§ГЫвдЦЕТЪОЭЪЧЦЕЪ§ЃЌЦЕЪ§Г§вдзмЪ§ОЭЪЧЦЕТЪЃЌМДПЩЕУГіД№АИЃЛдйИљОнЧѓГіЕФЦЕЪ§ЃЌМДПЩВЙШЋЭГМЦЭМЃЛ
ЃЈ2ЃЉАбИУаЁЧјгУЫЎСПВЛГЌЙ§15tЕФМвЭЅЕФЦЕТЪМгЦ№РДЃЌОЭПЩЕУЕНгУЫЎСПВЛГЌЙ§15tЕФМвЭЅеМБЛЕїВщМвЭЅзмЪ§ЕФАйЗжБШЃЛ
ЃЈ3ЃЉИљОнБэИёЧѓГідТОљгУЫЎСПдк![]() ЕФЦЕТЪЃЌНјЖјЧѓГідТОљгУЫЎСПГЌЙ§20tЕФЦЕТЪЃЌГЫвд1000МДПЩЕУЕННсЙћЃЎ
ЕФЦЕТЪЃЌНјЖјЧѓГідТОљгУЫЎСПГЌЙ§20tЕФЦЕТЪЃЌГЫвд1000МДПЩЕУЕННсЙћЃЎ
ЪдЬтНтЮіЃК(1)ЕїВщЕФМвЭЅзмЪ§ЪЧЃК6ЁТ0.12=50(ЛЇ)ЃЌ
дђдТгУЫЎСП![]() ЕФЦЕЪ§ЪЧЃК50ЁС0.24=12(ЛЇ)ЃЌ
ЕФЦЕЪ§ЪЧЃК50ЁС0.24=12(ЛЇ)ЃЌ
дТгУЫЎСП![]() ЕФЦЕТЪ
ЕФЦЕТЪ![]()
ЙЪД№АИЮЊЃК12ЃЌ0.08ЃЛ
ВЙШЋЕФЭМаЮШчЯТЭМЃК

(2)ИУаЁЧјгУЫЎСПВЛГЌЙ§15tЕФМвЭЅЕФЦЕТЪжЎКЭЪЧ0.12+0.24+0.32=0.68ЃЌ
МДдТОљгУЫЎСПВЛГЌЙ§15tЕФМвЭЅеМБЛЕїВщЕФМвЭЅзмЪ§ЕФ68%.
(3)дТОљгУЫЎСПдк![]() ЕФЦЕТЪЮЊ1(0.12+0.24+0.32+0.20+0.04)=0.08ЃЌ
ЕФЦЕТЪЮЊ1(0.12+0.24+0.32+0.20+0.04)=0.08ЃЌ
ЙЪдТОљгУЫЎСПГЌЙ§20tЕФЦЕТЪЮЊ0.08+0.04=0.12ЃЌ
дђИУаЁЧјдТОљгУЫЎСПГЌЙ§20tЕФМвЭЅДѓдМга1000ЁС0.12=120(ЛЇ).



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃН6ЃЌBCЃН8ЃЌЕуDЁЂEЗжБ№ЪЧаББпABКЭжБНЧБпBCЩЯЕФЕуЃЌАбЁїABCбизХжБЯпDEелЕўЃЌЖЅЕуBЕФЖдгІЕуЪЧЕуBЁфЃЎ
(1)ШчЭМЂйЃЌШчЙћЕуBЁфКЭЕуAжиКЯЃЌЧѓCEЕФГЄЃЎ
(2)ШчЭМЂкЃЌШчЙћЕуBЁфТфдкжБНЧБпACЕФжаЕуЩЯЃЌЧѓBEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
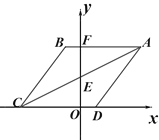
ЁОЬтФПЁПШчЭМЃЌвджБЯпABЩЯвЛЕуOЮЊЖЫЕузїЩфЯпOCЃЌЪЙЁЯAOCЃН65ЁуЃЌНЋвЛИіжБНЧШ§НЧаЮЕФжБНЧЖЅЕуЗХдкЕуOДІЃЎЃЈзЂЃКЁЯDOEЃН90ЁуЃЉ
ЃЈ1ЃЉШчЭМЂйЃЌШєжБНЧШ§НЧАхDOEЕФвЛБпODЗХдкЩфЯпOAЩЯЃЌдђЁЯCOEЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌНЋжБНЧШ§НЧАхDOEШЦЕуOЫГЪБеыЗНЯђзЊЖЏЕНФГИіЮЛжУЃЌШєOCЧЁКУЦНЗжЁЯAOEЃЌЧѓЁЯCODЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌНЋжБНЧШ§НЧАхDOEШЦЕуOШЮвтзЊЖЏЃЌШчЙћODЪМжедкЁЯAOCЕФФкВПЃЌЪдВТЯыЁЯAODКЭЁЯCOEгадѕбљЕФЪ§СПЙиЯЕЃПВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦпЃЈвЛЃЉАрЭЌбЇЮЊСЫНтФГаЁЧјМвЭЅдТОљгУЫЎЧщПіЃЌЫцЛњЕїВщСЫИУаЁЧјВПЗжМвЭЅЃЌВЂНЋЕїВщЪ§ОнећРэШчЯТБэЃЈВПЗжЃЉЃКШєИУаЁЧјга ![]() ЛЇМвЭЅЃЌОнДЫЙРМЦИУаЁЧјдТОљгУЫЎСПВЛГЌЙ§
ЛЇМвЭЅЃЌОнДЫЙРМЦИУаЁЧјдТОљгУЫЎСПВЛГЌЙ§ ![]() ЕФМвЭЅдМга
ЕФМвЭЅдМга
|
|
|
|
|
|
|
|
|
| ||
|
|
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊA=3a2b-2ab2+abcЃЌаЁУїЭЌбЇДэНЋЁА2A-BЁБПДГЩЁА2A+BЁБЃЌЫуЕУНсЙћЮЊ4a2b-3ab2+4abcЃЎ
ЃЈ1ЃЉЧѓГі2A-BЕФНсЙћЃЛ
ЃЈ2ЃЉаЁЧПЭЌбЇЫЕЃЈ1ЃЉжаЕФНсЙћЕФДѓаЁгыcЕФШЁжЕЮоЙиЃЌе§ШЗТ№ЃПШєa=![]() ЃЌb=
ЃЌb=![]() ЃЌЧѓЃЈ1ЃЉжаЪНзгЕФжЕЃЎ
ЃЌЧѓЃЈ1ЃЉжаЪНзгЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМе§ЗНаЮABCDжаЃЌЕуEЁЂFЗжБ№дкCDЁЂBCБпЩЯЃЌЁїAEFЪЧЕШБпШ§НЧаЮЃЎвдЯТНсТлЃКЂйECЃНFCЃЛЂкЁЯAEDЃН75ЁуЃЛЂлAFЃН![]() CEЃЛЂмEFЕФДЙжБЦНЗжЯпЪЧжБЯпACЃЎе§ШЗНсТлИіЪ§гаЃЈЁЁЁЁЃЉИіЃЎ
CEЃЛЂмEFЕФДЙжБЦНЗжЯпЪЧжБЯпACЃЎе§ШЗНсТлИіЪ§гаЃЈЁЁЁЁЃЉИіЃЎ

A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЃЌ
ЃЌ![]() СНЕудкЪ§жсЩЯЃЌЕу
СНЕудкЪ§жсЩЯЃЌЕу![]() БэЪОЕФЪ§ЮЊЃ10ЃЌЕу
БэЪОЕФЪ§ЮЊЃ10ЃЌЕу![]() ЕНЕу
ЕНЕу![]() ЕФОрРыЪЧЕу
ЕФОрРыЪЧЕу![]() ЕНЕу
ЕНЕу![]() ОрРыЕФ3БЖЃЌЕу
ОрРыЕФ3БЖЃЌЕу![]() вдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕу
вдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕу![]() ЯђгвдЫЖЏ.Еу
ЯђгвдЫЖЏ.Еу![]() вдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕу
вдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕу![]() ЯђгвдЫЖЏЃЈЕу
ЯђгвдЫЖЏЃЈЕу![]() ЁЂ
ЁЂ![]() ЭЌЪБГіЗЂЃЉ
ЭЌЪБГіЗЂЃЉ
![]()
ЃЈ1ЃЉЪ§жсЩЯЕу![]() ЖдгІЕФЪ§ЪЧ______.
ЖдгІЕФЪ§ЪЧ______.
ЃЈ2ЃЉОЙ§МИУыЃЌЕу![]() ЁЂЕу
ЁЂЕу![]() ЗжБ№ЕНдЕу
ЗжБ№ЕНдЕу![]() ЕФОрРыЯрЕШ.
ЕФОрРыЯрЕШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛСОЦћГЕааЪЛЪБЕФКФгЭСПЮЊ0.1Щ§/ЧЇУзЃЌШчЭМЪЧгЭЯфЪЃгргЭСП![]() ЃЈЩ§ЃЉЙигкМгТњгЭКѓвбааЪЛЕФТЗГЬ
ЃЈЩ§ЃЉЙигкМгТњгЭКѓвбааЪЛЕФТЗГЬ![]() ЃЈЧЇУзЃЉЕФКЏЪ§ЭМЯѓ.
ЃЈЧЇУзЃЉЕФКЏЪ§ЭМЯѓ.

ЃЈ1ЃЉИљОнЭМЯѓЃЌжБНгаДГіЦћГЕааЪЛ400ЧЇУзЪБЃЌгЭЯфФкЕФЪЃгргЭСПЃЌВЂМЦЫуМгТњгЭЪБгЭЯфЕФгЭСПЃЛ
ЃЈ2ЃЉЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂМЦЫуИУЦћГЕдкЪЃгргЭСП5Щ§ЪБЃЌвбааЪЛЕФТЗГЬ.
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂМЦЫуИУЦћГЕдкЪЃгргЭСП5Щ§ЪБЃЌвбааЪЛЕФТЗГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМOЮЊзјБъдЕуЃЌЫФБпаЮABCDЪЧСтаЮЃЌA(4ЃЌ4)ЃЌBЕудкЕкЖўЯѓЯоЃЌABЃН5ЃЌABгыyжсНЛгкЕуFЃЌЖдНЧЯпACНЛyжсгкЕуE
(1)жБНгаДГіBЁЂCЕуЕФзјБъЃЛ
(2)ЖЏЕуPДгCЕуГіЗЂвдУПУы1ИіЕЅЮЛЕФЫйЖШбиелЯпЖЮCЉDЉAдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌЧыгУКЌtЕФДњЪ§ЪНБэЪОЁїEDPЕФУцЛ§ЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌЪЧЗёДцдквЛЕуPЃЌЪЙЁїAPEбиЦфвЛБпЗелЙЙГЩЕФЫФБпаЮЪЧСтаЮЃПШєДцдкЃЌЧыжБНгаДГіЕБtЮЊЖрЩйУыЪБДцдкЗћКЯЬѕМўЕФЕуPЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com