练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．计算：（6m2n-3m2）÷3m=2mn-m．

    分析 根据整式的除法法则即可求出答案．

    解答 解：原式=2mn-m
    故答案为：2mn-m

    点评 本题考查整式的除法，解题的关键是熟练运用整式的运算法则，本题属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    10．已知：线段AB，BC，∠ABC=90°．
    求作：矩形ABCD．
    以下是甲、乙两同学的作业：

    老师说甲、乙同学的作图都正确．
    则甲的作图依据是：两组对边分别相等的四边形是平行四边形；有一个角是直角的平行四边形是矩形；
    乙的作图依据是：对角线互相平分的四边形是平行四边形；有一个角是直角的平行四边形是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．阅读下面材料，并解答其后的问题：
    定义：两组领边分别相等的四边形叫做筝形．
    如图1，四边形ABCD中，若AD=AB，CD=CB，则四边形ABCD是筝形．
    类比研究：
    我们在学完平行四边形后，知道可以从对称性、边、角和对角线四个角度对平行四边形的性质进行研究，请根据示例图形，完成下表：
    四边形示例图形对称性边角对角线
    平行
    四边形    		两组对边分别平行，两组对边分别相等两组对边分别平行，两组对边分别相等．两组对角
    分别相等．    		对角线互相平分．
    等腰
    梯形  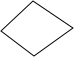  		①轴对称图形两组邻边分别相等有一组对角相等②一条对角线垂直平分另一条对角线
    （1）表格中①、②分别填写的内容是：
    ①轴对称图形；
    ②一条对角线垂直平分另一条对角线．
    （2）演绎论证：证明筝形有关对角线的性质．
    已知：在筝形ABCD中，AD=AB，BC=DC，AC、BD是对角线．
    求证：AC垂直平分BD．
    证明：
    （3）运用：如图3，已知筝形ABCD中，AD=AB=4，CD=CB，∠A=90°，∠C=60°，求筝形ABCD的面积

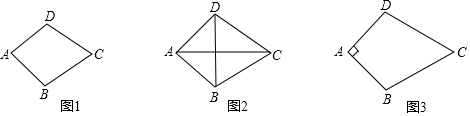
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

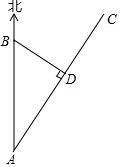    8．如图所示，沿海城市B的正南方向A处有一台风中心，沿AC的方向以30km/h的速度移动，已知AC所在的方向与正北成30°的夹角，B市距台风中心最短的距离BD为120km，求台风中心从A处到达D处需要多少小时？（$\sqrt{3}≈1.73$，结果精确到0.1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．等腰三角形一腰上的中线把该三角形的周长分成6cm和15cm两部分，求这个等腰三角形各边的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．计算：$\frac{2}{3}$$\sqrt{6}$•$\sqrt{3}$=2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．在分别写着“线段、钝角、直角三角形、等边三角形”的4张卡纸中，小刚从中任意抽取一张卡纸，抽到是轴对称图形的概率为$\frac{3}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．?ABCD的周长等于20，AB=6，则AD=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

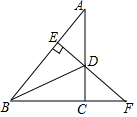    10．填空：把下面的推理过程补充完整，并在括号内注明理由．
    如图，在Rt△ABC中，∠ACB=90°，BD是∠ABC的平分线，DE⊥AB．垂足为E，ED的延长线交BC的延长线于点F．
    求证：AE=CF，∠A=∠F
    证明：∵∠ACB=90°（已知）
    ∴DC⊥BC（垂直的定义）
    又∵BD为∠ABC的平分线，DE⊥AB，（已知）
    ∴DC=DE （角平分线的性质）
    ∵在△ADE和△FDC中
    ∠DEA=∠DCF=90°　（垂直的定义）
    DE=DC（已证）
    ∠ADE=∠FDC（对顶角相等）
    ∴△ADE≌△FDC（ASA）
    ∴AE=CF （全等三角形的对应边相等）
    ∠A=∠F （全等三角形的对应角相等）．

    查看答案和解析>>

    同步练习册答案