在平面直角坐标系xOy中，直线y=kx（k为常数）与抛物线
交于A，B两点，且A点在y轴左侧，P点的坐标为（0，﹣4），连接PA，PB．有以下说法：
①PO2=PA•PB；
②当k＞0时，（PA+AO）（PB﹣BO）的值随k的增大而增大；
③当
时，BP2=BO•BA；
④△PAB面积的最小值为
．
其中正确的是 （写出所有正确说法的序号）
新非凡教辅冲刺100分系列答案科目：初中数学 来源： 题型：填空题
将二次函数
的图像向左平移2个单位再向下平移4个单位，所得函数表达式是
，我们来解释一下其中的原因：不妨设平移前图像上任意一点P经过平移后得到点P’，且点P’的坐标为
，那么P’点反之向右平移2个单位，再向上平移4个单位得到点
，由于点P是二次函数的图像上的点，于是把点P（x+2，y+4）的坐标代入再进行整理就得到.类似的，我们对函数
的图像进行平移：先向右平移1个单位，再向上平移3个单位，所得图像的函数表达式为_____.
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
如图，在平面直角坐标系xOy中，若动点P在抛物线y=ax2上，⊙P恒过点F（0，n），且与直线y=﹣n始终保持相切，则n= （用含a的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
今年，6月12日为端午节。在端午节前夕，三位同学到某超市调研一种进价为2元的粽子的销售情况。请根据小丽提供的信息，解答小华和小明提出的问题。
（1）小华的问题解答： ；
（2）小明的问题解答： 。
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
有一个二次函数的图象，三位学生分别说出了它的一些特点．
甲：对称轴是直线x=4；
乙：与x轴两交点的横坐标都是整数；
丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为3；
请写出满足上述全部特点的二次函数解析式：
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，已知直线
过点
和
，
是
轴正半轴上的动点，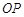
的垂直平分线交于点
，交轴于点
．
（1）直接写出直线的解析式；
（2）当
时，设
，
的面积为
，求S关于t的函数关系式；并求出S的最大值；
（3）当点Q在线段AB上（Q与A、B不重合）时，直线
过点A且与x轴平行，问在上是否存在点C，使得
是以为直角顶点的等腰直角三角形？若存在，求出点C的坐标，并证明；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（米）与水平距离
（米）之间的关系为
，由此可知铅球推出的距离是 ___米．
向上平移3个单位，再向左平移1个单位，则所得抛物线的解析式是 ．