
 如图,在△ABC中,AB=AC,D为边BC上一点,以AB、BD为邻边作平行四边形ABDE,连接AD、EC.若BD=CD,求证:四边形ADCE是矩形.
如图,在△ABC中,AB=AC,D为边BC上一点,以AB、BD为邻边作平行四边形ABDE,连接AD、EC.若BD=CD,求证:四边形ADCE是矩形. 科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛掷一枚硬币,硬币落地时正面朝上是随机事件 | |
| B. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| C. | 任意打开七年级下册数学教科书,正好是97页是确定事件 | |
| D. | 在相同条件下,只要试验的次数足够多,频率就可以作为概率的估计值 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=2,则AB=( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=2,则AB=( )| A. | 4 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
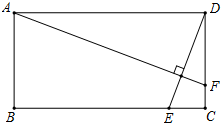 如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y.
如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com