

分析 (1)把点A、B的坐标分别代入函数解析式,列出关于系数b、c的方程组,通过解方程组求得它们的值即可;
(2)结合抛物线的解析式得到点C、N的坐标,利用B、C的坐标可以求得直线BC的解析式,由一次函数图象上点的坐标特征和点的坐标与图形的性质进行解答即可;
(3)根据P点在抛物线上设出P点,然后再由S△PAB=8,从而求出P点坐标.
解答 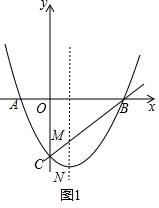 解:(1)如图1,∵抛物线y=x2+bx+c与x轴的两个交点分别为A(-1,0),B(3,0),
解:(1)如图1,∵抛物线y=x2+bx+c与x轴的两个交点分别为A(-1,0),B(3,0),
∴$\left\{\begin{array}{l}{(-1)^{2}-b+c=0}\\{{3}^{2}+3b+c=0}\end{array}\right.$,
解之得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
∴所求抛物线的解析式为:y=x2-2x-3;
(2)由(1)知,该抛物线的解析式为:y=x2-2x-3,则C(0,-3).
又∵y=x2-2x-3=(x-1)2-4,
∴N(1,-4).
设直线BC的解析式为y=kx-3(k≠0).
把B(3,0)代入,得
0=3k-3,
解得k=1,则该直线解析式为:y=x-3.
故当x=1时,y=-2,即M(1,-2),
∴MN=|-3|-|-2|=1.即MN=1;
(3)设点P的坐标为(x,y),由题意,得
S△PAB=$\frac{1}{2}$×4×|y|=8,
∴|y|=4,
∴y=±4.
当y=4时,x2-2x-3=4,
∴x1=1+2$\sqrt{2}$,x2=1-2$\sqrt{2}$,
当y=-4时,x2-2x-3=-4,
∴x=1,
∴当P点的坐标分别为(1+2$\sqrt{2}$,4)、(1-2$\sqrt{2}$,4)、(1,-4)时,S△PAB=8.
点评 本题考查了二次函数综合题.
第(1)题考查用待定系数法求二次函数的解析式,比较简单;
第(2)题考查了待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,抛物线解析式的三种形式间的转化;
第(2)题主要考查函数的性质及函数图象点的坐标,把三角形面积公式同函数联系起来,是一种比较常见的题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
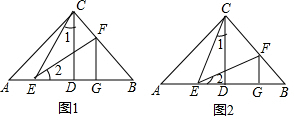 【问题情境】一节数学课后,老师布置了一道课后练习题:
【问题情境】一节数学课后,老师布置了一道课后练习题: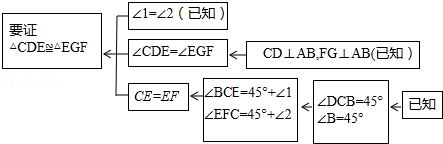
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
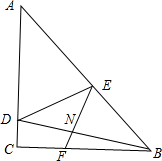 如图,在△ABC中,∠ACB=90°,AC=BC,在AC上取一点D,AB上取一点E,使∠BDC=∠EDA,过点E作EF⊥BD垂足为N,并与BC交于点F.若CF=4,AD=$\frac{11}{2}$,则CD=$\frac{3}{2}$.
如图,在△ABC中,∠ACB=90°,AC=BC,在AC上取一点D,AB上取一点E,使∠BDC=∠EDA,过点E作EF⊥BD垂足为N,并与BC交于点F.若CF=4,AD=$\frac{11}{2}$,则CD=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示是上海东方明珠广播电视塔的一部分,若塔座所形成的直角三角形的直角边长分别是a,b,则斜边长为$\sqrt{{a}^{2}+{b}^{2}}$,圆形的球体在平面图上的面积为S,则半径为$\frac{\sqrt{πS}}{π}$.
如图所示是上海东方明珠广播电视塔的一部分,若塔座所形成的直角三角形的直角边长分别是a,b,则斜边长为$\sqrt{{a}^{2}+{b}^{2}}$,圆形的球体在平面图上的面积为S,则半径为$\frac{\sqrt{πS}}{π}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com