
分析 先解不等式3x+b<1时,得x<$\frac{1-b}{3}$;再求出函数y=3x+b沿x轴翻折后的解析式为y=-3x-b,解不等式-3x-b<1,得x>-$\frac{1+b}{3}$;根据x满足0<x<2,得出-$\frac{1+b}{3}$=0,$\frac{1-b}{3}$=2,进而求出b的取值范围.
解答 解:∵y=3x+b,
∴当y<1时,3x+b<1,解得x<$\frac{1-b}{3}$;
∵函数y=3x+b沿x轴翻折后的解析式为-y=3x+b,即y=-3x-b,
∴当y<1时,-3x-b<1,解得x>-$\frac{1+b}{3}$;
∴-$\frac{1+b}{3}$<x<$\frac{1-b}{3}$,
∵x满足0<x<2,
∴-$\frac{1+b}{3}$=0,$\frac{1-b}{3}$=2,
∴b=-1,b=-5,
∴b的取值范围为-5≤b≤-1.
故答案为-5≤b≤-1.
点评 本题考查了一次函数图象与几何变换,求出函数y=3x+b沿x轴翻折后的解析式是解题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
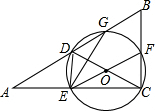 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com