
分析 利用抛物线的顶点坐标得到抛物线与x轴的两交点坐标为(1,0),(5,0),则可设交点式y=a(x-1)(x-5),然后把顶点坐标代入求出a的值即可.
解答 解:根据题意得抛物线的对称轴为直线x=3,
∵抛物线在x轴上截得的线段长为4,
∴抛物线与x轴的两交点坐标为(1,0),(5,0),
设抛物线解析式为y=a(x-1)(x-5),
把(3,-2)代入得a•2•(-2)=-2,
解得:a=$\frac{1}{2}$,
∴抛物线解析式为y=$\frac{1}{2}$(x-1)(x-5),
即y=$\frac{1}{2}$x2-3x+$\frac{5}{2}$.
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
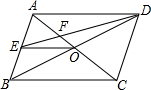 如图,O为?ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S四边形ABCD=12,则S△BOE的值为$\frac{3}{2}$.
如图,O为?ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S四边形ABCD=12,则S△BOE的值为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
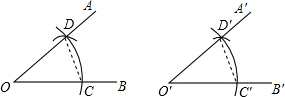 利用直尺和圆规作一个角等于已知角的作法如下:
利用直尺和圆规作一个角等于已知角的作法如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
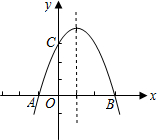 如图所示的抛物线是由抛物线y=-x2向上平移4个单位长度,再向右平移1个单位长度得到,与y轴交于C点.
如图所示的抛物线是由抛物线y=-x2向上平移4个单位长度,再向右平移1个单位长度得到,与y轴交于C点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com