
【题目】如图是平面直角坐标系及其中的一条直线,该直线还经过点C(3,﹣10).
(1)求这条直线的解析式;
(2)若该直线分别与x轴、y轴交于A、B两点,点P在x轴上,且S△PAB=6S△OAB,求点P的坐标.

【答案】(1)直线的解析式为:y=﹣3x﹣1;(2)点P的坐标为P(![]() ,0)或P(﹣
,0)或P(﹣![]() ,0).
,0).
【解析】试题分析:(1)待定系数法求解可得;
(2)先根据直线解析式求得A、B点坐标,进而可得S△OAB=![]() ,设点P的坐标为P(m,0),用含m的式子表示出S△PAB,根据S△PAB=6S△OAB可得关于m的方程,解方程即可得.
,设点P的坐标为P(m,0),用含m的式子表示出S△PAB,根据S△PAB=6S△OAB可得关于m的方程,解方程即可得.
试题解析:(1)设直线的解析式为:y=kx+b,
由图可知,直线经过点(﹣1,2),
又已知经过点C(3,﹣10),
分别把坐标代入解析式中,得: ![]() ,解得
,解得![]() ,
,
∴直线的解析式为:y=﹣3x﹣1;
(2)由y=﹣3x﹣1,令y=0,
解得x=﹣![]() ;
;
令x=0,解得y=﹣1.
∴A、B两点的坐标分别为A(﹣![]() ,0)、B(0,﹣1).
,0)、B(0,﹣1).
S△OAB=![]() OAOB=
OAOB=![]() ×
×![]() ×1=
×1=![]() .
.
设点P的坐标为P(m,0),
则S△PAB=![]() PAOB=
PAOB=![]() ×|m﹣(﹣
×|m﹣(﹣![]() )|×1=
)|×1=![]() |m+
|m+![]() |,
|,
由S△PAB=6S△OAB,得![]() |m+
|m+![]() |=6×
|=6×![]() ,
,
从而得m+![]() =2或m+
=2或m+![]() =﹣2,
=﹣2,
∴m=![]() 或m=﹣
或m=﹣![]() ,
,
即点P的坐标为P(![]() ,0)或P(
,0)或P(![]() ,0).
,0).


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】2015年全球葵花籽产量约为4200万吨,比2014年上涨2.1%,某企业加工并销售葵花籽,假设销售量与加工量相等,在图中,线段AB、折线CDB分别表示葵花籽每千克的加工成本y1(元)、销售价y2(元)与产量x(kg)之间的函数关系;
(1)请你解释图中点B的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的y1与x之间的函数解析式;
(3)当0<x≤90时,求该葵花籽的产量为多少时,该企业获得的利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织初一、初二学生举行“四城同创”宣传活动,从学校坐车出发,先上坡到达A地后,宣传8分钟;然后下坡到B地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度保持不变,在A地仍要宣传8分钟,则他们从B地返回学校用的时间是( )
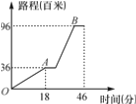
A. 48分钟 B. 45.2分钟 C. 46分钟 D. 33分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线y=﹣x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα﹣tanβ=2,OC2=OAOB.
(1)△ABC是否为直角三角形?若是,请给出证明;若不是,请说明理由;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积.
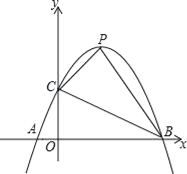
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P是直线l外一点, A、B、C是直线l上一点,且PA=5,PB=3,PC=2,那么点P到直线l的距离为( ).
A. 等于2 B. .大于2C. 小于或等于2D. 小于2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com