
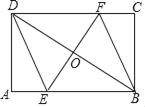
【题目】如图,在矩形ABCD中,AB=8,BC=4,过对角线BD的中点O的直线分别交AB、CD于点E、F,连接DE,BF.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)根据平行四边形ABCD的性质,判定△BOE≌△DOF(ASA),得出四边形BEDF的对角线互相平分,进而得出结论;
(2)在Rt△ADE中,由勾股定理得出方程,解方程求出BE,由勾股定理求出BD,得出OB,再由勾股定理求出EO,即可得出EF的长.
详解:(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF.
在△BOE和△DOF中, ,
,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形.
(2)解:当四边形BEDF是菱形时,BD⊥EF,
设BE=x,则DE=x,AE=8﹣x.
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(8﹣x)2,
解得x=5,即BE=5.
∵BD=![]() =
=![]() =4
=4![]() ,
,
∴OB=![]() BD=2
BD=2![]() .
.
∵BD⊥EF,
∴EO=![]() =
=![]() =
=![]() ,
,
∴EF=2EO=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;…;若在第n次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=3,BC=9,则称矩形ABCD为2阶奇异矩形.
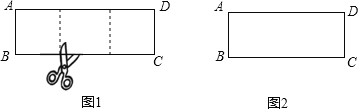
(1)判断与操作:
如图2,矩形ABCD长为7,宽为3,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.
(2)探究与计算:
已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法:
(1)“快车”行驶里程不超过5公里计费8元;
(2)“顺风车”行驶里程超过2公里的部分,每公里计费1.2元;
(3)A点的坐标为(6.5,10.4);
(4)从哈尔滨西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东24.5°方向,轮船向正东航行了2400m,到达Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A、B间的距离(参考数据cos41°=0.75).
查看答案和解析>>
科目:初中数学 来源: 题型:
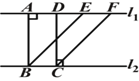
【题目】如图,![]() ∥
∥![]() ,BE∥CF,BA⊥
,BE∥CF,BA⊥![]() ,DC⊥
,DC⊥![]() ,下面给出四个结论:①BE=CF;②AB=DC;③
,下面给出四个结论:①BE=CF;②AB=DC;③![]() ;
;
④四边形ABCD是矩形.其中说法正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
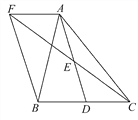
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
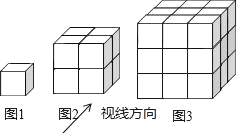
【题目】如图所示,每个小立方体的棱长为1,按如图所示的视线方向看,图1中共有1个1立方体,其中1个看得见,0个看不见;图2中共有8个立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;…,则第11个图形中,其中看得见的小立方体个数是( )
A. 271 B. 272 C. 331 D. 332
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com