
��֪������x��һԪ���η���mx2����4m+1��x+3m+3="0" ��m��1����
��1����֤����������������ȵ�ʵ������
��2���跽�̵�����ʵ�����ֱ�Ϊx1��x2������x1��x2������y�ǹ���m�ĺ�������y=x1��3x2������������Ľ���ʽ��
��3������2�������õĺ�����ͼ����ֱ��m=2����ಿ����ֱ��m=2���ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ������������µ�ͼ��ش𣺵�����m�ĺ���y=2m+b��ͼ�����ͼ��������������ʱ��b��ȡֵ��Χ��
��1��֤������������2��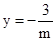 ����3��
����3��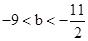 ��
��
���������������1�������ͻ�ƿ��������á�������ó�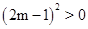 �ó�����0���Ӷ���������������ȵ�ʵ������
�ó�����0���Ӷ���������������ȵ�ʵ������
��2���������ʽ�ó�x�Ľ⣬��y=x1��3x2���������m�Ľ���ʽ��
��3����������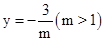 ��ͼ����ͼ����ֱ��m=2��ಿ���ش�ֱ�߷��ۣ�������ͼ����ͼ��ʾ����֪��A��B������ֱ�Ϊ
��ͼ����ͼ����ֱ��m=2��ಿ���ش�ֱ�߷��ۣ�������ͼ����ͼ��ʾ����֪��A��B������ֱ�Ϊ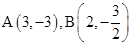 �����ֱ��
�����ֱ��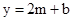 ����A��Bʱ��
����A��Bʱ�� ��ֵ������֮�伴Ϊ����
��ֵ������֮�伴Ϊ����
��1��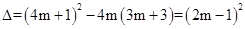 ��
��
��m��1��
��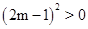
�������������ʵ����
��2��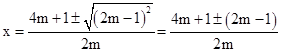
�������ֱ�Ϊ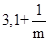 ��
��
��m��1��
��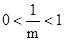 ����
����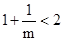 ��
��
��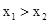 ��
��
��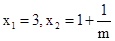 ��
��
��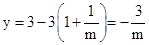 ��
��
��3����������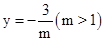 ��ͼ����ͼ����ֱ��m=2��ಿ���ش�ֱ�߷��ۣ�������ͼ����ͼ��ʾ����֪��A��B������ֱ�Ϊ
��ͼ����ͼ����ֱ��m=2��ಿ���ش�ֱ�߷��ۣ�������ͼ����ͼ��ʾ����֪��A��B������ֱ�Ϊ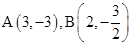 ��
��
��ֱ��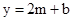 ����Aʱ��
����Aʱ��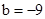 ��
��
��ֱ��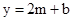 ����Bʱ��
����Bʱ��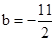 ��
��
��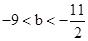 ��
��
���㣺1��һ�κ����ͷ����������ۺ��⣻2��һԪ���η��̸����б�ʽ��3����һԪ���η��̣�4�����۶ԳƵ����ʣ�


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��һ�κ���y=x+b��ͼ���뷴��������y= ��x��0����ͼ���ڵ�A��2��1������x�ύ�ڵ�B��
��x��0����ͼ���ڵ�A��2��1������x�ύ�ڵ�B��
��1����k��b��ֵ��
��2������OA�����AOB�������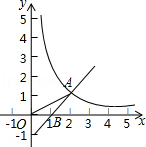
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��һ�κ���y1=kx+b��ͼ���뷴��������y2= ��ͼ���ཻ�ڵ�A(2,5)�͵�B,��y���ཻ�ڵ�C(0��7).
��ͼ���ཻ�ڵ�A(2,5)�͵�B,��y���ཻ�ڵ�C(0��7).
��1���������������Ľ���ʽ��
��2����xȡ��ֵʱ��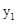 ��
��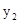 .
.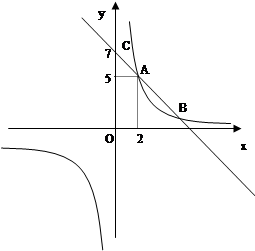
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ��� ��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B����֪
��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B����֪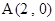 ��
��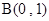 ����C��-2��m����ֱ��AB�ϣ�����������
����C��-2��m����ֱ��AB�ϣ�����������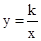 ��ͼ����C��
��ͼ����C��
��1����һ�κ����������������Ľ���ʽ��
��2�����ͼ��ֱ��д������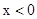 ʱ������ʽ
ʱ������ʽ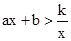 �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ֱ֪��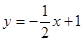 ��x�ᡢy��ֱ���B�㡢A�㣬ֱ��
��x�ᡢy��ֱ���B�㡢A�㣬ֱ�� ��x�ᡢy��ֱ���D�㡢E�㣬����ֱ�߽��ڵ�C����SBCD�����Բֱ���ij��ȡ�
��x�ᡢy��ֱ���D�㡢E�㣬����ֱ�߽��ڵ�C����SBCD�����Բֱ���ij��ȡ�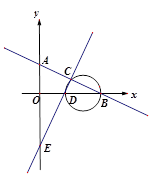
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��ֱ��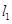 ,
,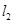 �ཻ�ڵ�
�ཻ�ڵ�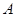 ��
��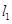 ��
��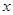 ��Ľ�������Ϊ
��Ľ�������Ϊ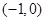 ��
��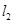 ��
��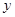 ��Ľ�������Ϊ
��Ľ�������Ϊ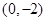 �����ͼ�����������⣺��ÿС��4�֣���8�֣�
�����ͼ�����������⣺��ÿС��4�֣���8�֣�
��1����ֱ��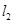 ��ʾ��һ�κ����ı���ʽ��
��ʾ��һ�κ����ı���ʽ��
��2����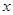 Ϊ��ֵʱ��
Ϊ��ֵʱ��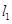 ,
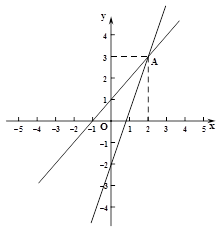
,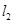 ��ʾ������һ�κ���ֵ������
��ʾ������һ�κ���ֵ������ .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ƽ��ֱ������ϵxOy�У�������������P1��x1��y1����P2��x2��y2���ġ��dz����롱���������¶��壺
��|x1��x2|��|y1��y2|�����P1���P2�ġ��dz����롱Ϊ|x1��x2|��
��|x1��x2|��|y1��y2|�����P1���P2�ġ��dz����롱Ϊ|y1��y2|��
���磺��P1��1��2������P2��3��5������Ϊ|1��3|��|2��5|�����Ե�P1���P2�ġ��dz����롱Ϊ|2��5|=3��Ҳ����ͼ1���߶�P1Q���߶�P2Q���ȵĽϴ�ֵ����QΪ��ֱ��y���ֱ��P1Q�봹ֱ��x���ֱ��P2Q���㣩��
��1����֪��A���� ��0����BΪy���ϵ�һ�����㣬
��0����BΪy���ϵ�һ�����㣬
������A���B�ġ��dz����롱Ϊ2��д��һ�����������ĵ�B�����ꣻ
��ֱ��д����A���B�ġ��dz����롱����Сֵ��
��2����֪C��ֱ��y=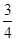 x+3�ϵ�һ�����㣬
x+3�ϵ�һ�����㣬
����ͼ2����D�������ǣ�0��1�������C���D�ġ��dz����롱����Сֵ����Ӧ�ĵ�C�����ꣻ
����ͼ3��E����ԭ��OΪԲ�ģ�1Ϊ�뾶��Բ�ϵ�һ�����㣬���C���E�ġ��dz����롱����Сֵ����Ӧ�ĵ�E���C�����꣮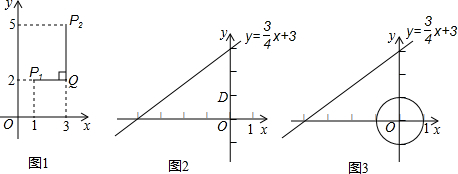
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪һ�κ����뷴����������ͼ���ڵ�A(��4����2)��B(a��4)��
(1)���������Ľ���ʽ�͵�B�����ꣻ
(2)����ͼ��ش𣬵�x��ʲô��Χ��ʱ��һ�κ�����ֵ���ڷ�����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
Ϊ����ѧ�������������εĸ߶ȶ��ǰ�һ���Ĺ�ϵ������Ƶģ��о���������������ĸ߶�Ϊ cm�����ӵĸ߶�Ϊ
cm�����ӵĸ߶�Ϊ cm����
cm����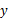 Ӧ��
Ӧ��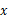 ��һ�κ������±��г������������Ŀ����εĸ߶ȣ�
��һ�κ������±��г������������Ŀ����εĸ߶ȣ�
| | ��һ�� | �ڶ��� |
���Ӹ߶�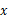 ��cm�� ��cm�� | 40 | 37 |
�����߶�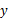 ��cm�� ��cm�� | 75 | 70 |
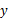 ��
��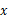 �ĺ�����ϵʽ��
�ĺ�����ϵʽ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com