
如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,扇形纸片DOE的顶点O与边AB的中点重合,OD交BC于点F,OE经过点C,且∠DOE=∠B.
(1)证明△COF是等腰三角形,并求出CF的长;
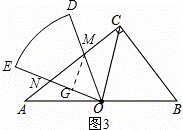
(2)将扇形纸片DOE绕点O逆时针旋转,OD,OE与边AC分别交于点M,N(如图2),当CM的长是多少时,△OMN与△BCO相似?
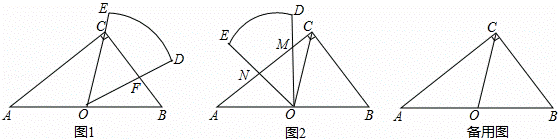
解:(1)∵∠ACB=90°,点O是AB的中点,
∴OC=0B=OA=5.
∴∠OCB=∠B,∠ACO=∠A.
∵∠DOE=∠B,
∴∠FOC=∠OCF.
∴FC=FO.
∴△COF是等腰三角形.
过点F作FH⊥OC,垂足为H,如图1,
∵FC=FO,FH⊥OC,
∴CH=OH=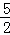 ,∠CHF=90°.
,∠CHF=90°.
∵∠HCF=∠B,∠CHF=∠BCA=90°,
∴△CHF∽△BCA.
∴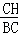 =
=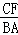 .
.
∵CH=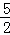 ,AB=10,BC=6,
,AB=10,BC=6,
∴CF=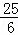 .
.
∴CF的长为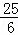 .
.
(2)①若△OMN∽△BCO,如图2,
则有∠NMO=∠OCB.
∵∠OCB=∠B,
∴∠NMO=∠B.
∵∠A=∠A,
∴△AOM∽△ACB.
∴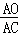 =
= .
.
∵∠ACB=90°,AB=10,BC=6,
∴AC=8.
∵AO=5,AC=8,AB=10,
∴AM=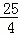 .
.
∴CM=AC﹣AM=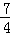 .
.
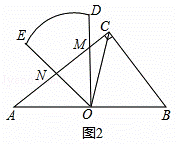
②若△OMN∽△BOC,如图3,
则有∠MNO=∠OCB.
∵∠OCB=∠B,
∴∠MNO=∠B.
∵∠ACO=∠A,
∴△CON∽△ACB.
∴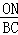 =
=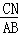 =
=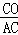 .
.
∵BC=6,AB=10,AC=8,CO=5,
∴ON=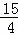 ,CN=
,CN=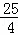 .
.
过点M作MG⊥ON,垂足为G,如图3,
∵∠MNO=∠B,∠MON=∠B,
∴∠MNO=∠MON.
∴MN=MO.
∵MG⊥ON,即∠MGN=90°,
∴NG=OG=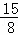 .
.
∵∠MNG=∠B,∠MGN=∠ACB=90°,
∴△MGN∽△ACB.
∴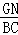 =
=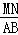 .
.
∵GN=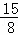 ,BC=6,AB=10,
,BC=6,AB=10,
∴MN=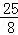 .
.
∴CM=CN﹣MN=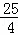 ﹣
﹣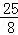 =
=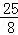 .
.
∴当CM的长是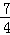 或
或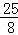 时,△OMN与△BCO相似.
时,△OMN与△BCO相似.



科目:初中数学 来源: 题型:
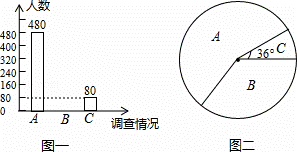
为了了解学生毕业后就读普通高中或就读中等职业技术学校的意向,某校对八、九年级部分学生进行了一次调查,调查结果有三种情况:A.只愿意就读普通高中;B.只愿意就读中等职业技术学校;C.就读普通高中或中等职业技术学校都愿意.学校教务处将调查数据进行了整理,并绘制了尚不完整的统计图如下,请根据相关信息,解答下列问题:
(1)本次活动共调查了多少名学生?
(2)补全图一,并求出图二中B区域的圆心角的度数;
(3)若该校八、九年级学生共有2800名,请估计该校学生只愿意就读中等职业技术学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两支仪仗队的队员人数相同,平均身高相同,身高的方差分别为S2甲=0.9,S2乙=1.1,则甲、乙两支仪仗队的队员身高更整齐的是 (填“甲”或“乙”).
查看答案和解析>>
科目:初中数学 来源: 题型:
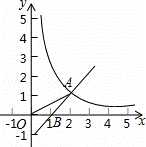
如图,一次函数y=x+b的图象与反比例函数y=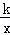 (x>0)的图象交于点A(2,1),与x轴交于点B.
(x>0)的图象交于点A(2,1),与x轴交于点B.
(1)求k和b的值;
(2)连接OA,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com