
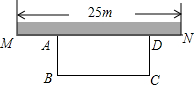
 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,分析 (1)根据题意可以得到相应的一元二次方程,从而可以解答本题;
(2)根据题意可以得到面积与矩形一边长的关系式,然后化为顶点式,注意求出的边长要符合题意.
解答 解:(1)设AB为xm,则BC为(50-2x)m,
x(50-2x)=300,
解得,x1=10,x2=15,
当x1=10时50-2x=30>25(不合题意,舍去),
当x2=15时50-2x=20<25(符合题意),
答:当砌墙宽为15米,长为20米时,花园面积为300平方米;
(2)设AB为xm,矩形花园的面积为ym2
则y=x(50-2x)=-2(x-$\frac{25}{2}$)2+$\frac{625}{2}$,
∴x=$\frac{25}{2}$时,此时y取得最大值,50-2x=25符合题意,此时y=$\frac{625}{2}$,
即当砌墙的宽为$\frac{25}{2}$米,长为25米时,矩形花园的面积最大.
点评 本题考查二次函数的应用、一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:填空题
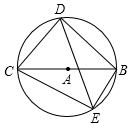 如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$.
如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
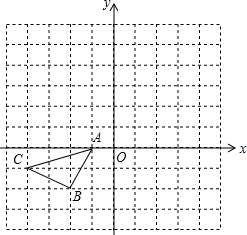 在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.
在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
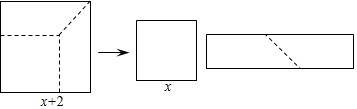
| A. | 2x+2 | B. | 4x+4 | C. | x+4 | D. | 2x-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com