已知点A(a,y1)、B(2a,y2)、C(3a,y3)都在抛物线y=5x2+12x上.
(1)求抛物线与x轴的交点坐标;
(2)当a=1时,求△ABC的面积;
(3)是否存在含有y1,y2,y3,且与a无关的等式?如果存在,试给出一个,并加以证明;如果不存在,说明理由.
【答案】
分析:(1)令y=0,得出的关于x的二元一次方程的解就是抛物线与x轴的交点的横坐标,也就求得出了抛物线与x轴的交点坐标.
(2)当a=1时,根据抛物线的解析式求出A、B、C三点的坐标,由于三角形的面积无法直接求出,因此通过作辅助线用其他规则图形的面积的“和,差”关系来求.如:分别过点A、B、C作x轴的垂线,垂足分别为D、E、F,S
△ABC=S
梯形ADFC-S
梯形ADEB-S
梯形BEFC由此可求出△ABC的面积.
(3)可将A、B、C三点的坐标代入抛物线中,得出y
1,y
2,y
3的值,然后进行比较即可得出它们之间的和差或倍数关系.
解答: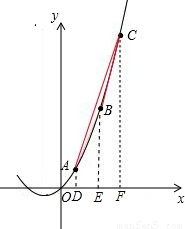
解:(1)由5x
2+12x=0,
得x
1=0,

.
∴抛物线与x轴的交点坐标为(0,0)、(
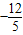
,0).
(2)当a=1时,得A(1,17)、B(2,44)、C(3,81),
分别过点A、B、C作x轴的垂线,垂足分别为D、E、F,
则有S
△ABC=S
梯形ADFC-S
梯形ADEB-S
梯形BEFC=

-

-

=5(个单位面积)
(3)如:y
3=3(y
2-y
1).
事实上,y
3=5×(3a)
2+12×(3a)=45a
2+36a.
3(y
2-y
1)=3[5×(2a)
2+12×2a-(5a
2+12a)]=45a
2+36a.
∴y
3=3(y
2-y
1).
点评:本题主要考查了二次函数的应用,根据抛物线的解析式来确定A、B、C三点的坐标是解题的关键.

 解:(1)由5x2+12x=0,
解:(1)由5x2+12x=0, .
.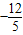 ,0).
,0). -
- -
- =5(个单位面积)
=5(个单位面积)
