
【题目】如图,在矩形ABCD中,![]() ,
,![]() ,将矩形沿直线EF折叠.使得点A恰好落在BC边上的点G处,且点E、F分别在边AB、AD上(含端点),连接CF.
,将矩形沿直线EF折叠.使得点A恰好落在BC边上的点G处,且点E、F分别在边AB、AD上(含端点),连接CF.
(1)当![]() 时,求AE的长;
时,求AE的长;
(2)当AF取得最小值时,求折痕EF的长;
(3)连接CF,当![]() 是以CG为底的等腰三角形时,直接写出BG的长.
是以CG为底的等腰三角形时,直接写出BG的长.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据折叠得出AE=EG,据此设AE=EG=x,则有BE=6-x,由勾股定理求解可得;
(2)由FG⊥BC时FG的值最小,即此时AF能取得最小值,显然四边形AEGF是正方形,从而根据勾股定理可得答案;
(3)由△CFG是以FG为一腰的等腰三角形,可知应分两种情况讨论:①FG=FC;②FG=GC;分别求解可得.
(1)由折叠易知,![]() ,设
,设![]() ,则有
,则有![]() ,
,
由勾股定理,得![]() ,解得
,解得![]() ,即
,即![]()
(2)由折叠易知,![]() ,而当
,而当![]() 时,FG的值最小,即此时AF能取得最小值,
时,FG的值最小,即此时AF能取得最小值,
![]() 当
当![]() 时,FG的值最小,即此时AF能取得最小值,
时,FG的值最小,即此时AF能取得最小值,
![]() 当
当![]() 时,点E与点B重合,
时,点E与点B重合,
此时四边形AEGF是正方形,
![]() 折痕
折痕![]() .
.
(3)由△CFG是以FG为一腰的等腰三角形,可知应分两种情况讨论:
①当FG=FC时,如图2,过F作FH⊥CG于H,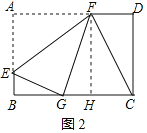
则有:AF=FG=FC,CH=DF=GH
设AF=FG=FC=x,则DF=10-x=CH=GH
在Rt△CFH中
∵CF2=CH2+FH2
∴x2=62+(10-x)2
解得:x=![]() ,
,
∴DF=CH=GH=10-![]() ,
,
即BG=10-![]() ×2=
×2=![]() ,
,
②当FG=GC时,则有:AF=FG=GC=x,CH=DF=10-x;
∴GH=x-(10-x)=2x-10,
在Rt△FGH中,由勾股定理易得:x2=62+(2x-10)2,
化简得:3x2-40x+136=0,
∵△=(-40)2-4×3×136=-32<0,
∴此方程没有实数根.
综上可知:BG=![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】春华中学为了解九年级学生的身高情况,随机抽测50名学生的身高后,所得部分资料如下(身高单位:![]() ,测量时精确到
,测量时精确到![]() ):
):
身高 | 148 | 151 | 154 | 155 | 157 | 158 | 160 | 161 | 162 | 164 |
人数 | 1 | 1 | 2 | 1 | 2 | 3 | 4 | 3 | 4 | 5 |
身高 | 165 | 166 | 167 | 168 | 170 | 171 | 173 | 175 | 177 | 179 |
人数 | 2 | 3 | 6 | 1 | 4 | 2 | 3 | 1 | 1 | 1 |
若将数据分成8组,取组距为![]() ,相应的频率分布表(部分)是:
,相应的频率分布表(部分)是:
分组 | 频数 | 频率 |
147.5~151.5 | 2 | 0.04 |
151.5~155.5 | 3 | 0.06 |
155.5~159.5 | 5 | 0.10 |
159.5~163.5 | 11 | 0.22 |
163.5~167.5 | ________ | ________ |
167.5~171.5 | 7 | 0.14 |
171.5~175.5 | 4 | 0.08 |
175.5~179.5 | 2 | 0.04 |
合计 | 50 | 1.00 |
请回答下列问题:
(1)样本数据中,学生身高的众数、中位数各是多少?
(2)填写频率分布表中未完成的部分;
(3)若该校九年级共有850名学生,请你估计该年级学生身高在![]() 及以上的人数.
及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三张卡片的正面分别写有数字2,5,5,卡片除数字外完全相同,将它们洗匀后,背面朝上放置在桌面上.
(1)从中任意抽取一张卡片,该卡片上数字是5的概率为 ;
(2)学校将组织部分学生参加夏令营活动,九年级(1)班只有一个名额,小刚和小芳都想去,于是利用上述三张卡片做游戏决定谁去,游戏规则是:从中任意抽取一张卡片,记下数字放回,洗匀后再任意抽取一张,将抽取的两张卡片上的数字相加,若和等于7,小钢去;若和等于10,小芳去;和是其他数,游戏重新开始.你认为游戏对双方公平吗?请用画树状图或列表的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:已知二次函数![]() 经过点
经过点![]() .
.
(1)求该函数的表达式;
(2)如图所示,点![]() 是抛物线上在第二象限内的一个动点,且点
是抛物线上在第二象限内的一个动点,且点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①求![]() 的面积
的面积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②求![]() 的面积的最大值,并求出此时点
的面积的最大值,并求出此时点![]() 的坐标.
的坐标.
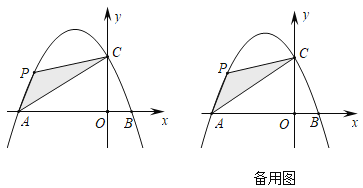
拓展:在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有两个不同的交点,请直接写出
有两个不同的交点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
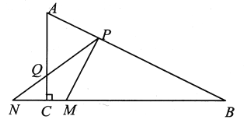
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() ,
,![]() 同时从点
同时从点![]() 出发,分别沿射线
出发,分别沿射线![]() ,
,![]() 方向运动,且满足
方向运动,且满足![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,
,![]() 与直线
与直线![]() 交于点
交于点![]() .设
.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 之间的函数图象大致是( )
之间的函数图象大致是( )
A. 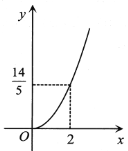 B.
B. 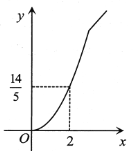 C.
C. 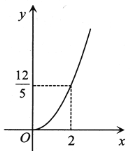
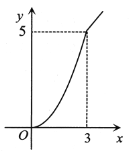
查看答案和解析>>
科目:初中数学 来源: 题型:
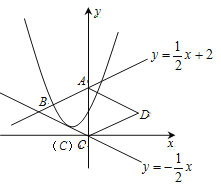
【题目】如图,直线![]() 与y轴交于点A,与直线
与y轴交于点A,与直线![]() 交于点B,以AB为边向右做菱形ABCD,点C恰与原点重合,抛物线
交于点B,以AB为边向右做菱形ABCD,点C恰与原点重合,抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,若抛物线与菱形的边AB,BC都有公共点,则h的取值范围是( )
上移动,若抛物线与菱形的边AB,BC都有公共点,则h的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
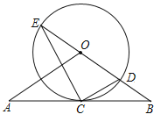
【题目】已知:如图,在△OAB中,OA=OB,⊙O经过AB的中点C,与OB交于点D,且与BO的延长线交于点E,连接EC,CD.
(1)试判断AB与⊙O的位置关系,并加以证明;
(2)若tanE=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com