
分析 由两函数的交点坐标为(m,n),将x=m,y=n代入反比例解析式,求出mn的值,代入一次函数解析式,得出n-m的值,将所求式子通分并利用同分母分式的加法法则计算后,把mn及n-m的值代入即可求出值.
解答 解:∵函数y=-$\frac{3}{x}$与y=y=x+2的图象的交点坐标是(m,n),
∴将x=m,y=n代入反比例解析式得:mn=-3,
代入一次函数解析式得:n=m+2,即n-m=2,
则$\frac{1}{m}-\frac{1}{n}$=$\frac{n-m}{mn}$=$\frac{2}{-3}$=-$\frac{2}{3}$.
故答案为:-$\frac{2}{3}$.
点评 此题考查了反比例函数与一次函数的交点问题,其中将x=m,y=n代入两函数解析式得出关于m与n的关系式是解本题的关键.


科目:初中数学 来源: 题型:解答题
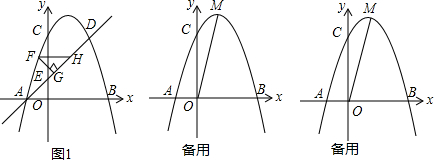
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
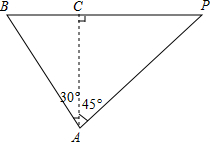 如图,一艘轮船原在A处,它的北偏东45方向上有一灯塔P,轮船沿着北偏西30方向航行4小时到达B处,这时灯塔P正好在轮船的正东方向上,已知轮船的速度为25海里/时.求轮船在B处时与灯塔P的距离(结果保留根号).
如图,一艘轮船原在A处,它的北偏东45方向上有一灯塔P,轮船沿着北偏西30方向航行4小时到达B处,这时灯塔P正好在轮船的正东方向上,已知轮船的速度为25海里/时.求轮船在B处时与灯塔P的距离(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
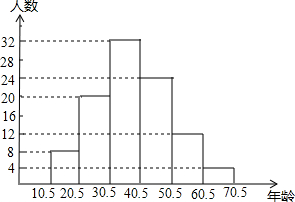 今年6月南博会在我市成功举办,吸引了众多的国内外人士,期间,对六家大宾馆、饭店中游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成条形统计图,如图所示,请结合图形回答下列问题:
今年6月南博会在我市成功举办,吸引了众多的国内外人士,期间,对六家大宾馆、饭店中游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成条形统计图,如图所示,请结合图形回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
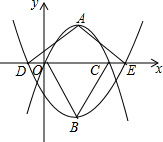 如图,在平面直角坐标系中,抛物线y=a1(x-2)2+2与y=a2(x-2)2-3的顶点分别为A,B,与x轴分别交于点O,C,D,E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1.
如图,在平面直角坐标系中,抛物线y=a1(x-2)2+2与y=a2(x-2)2-3的顶点分别为A,B,与x轴分别交于点O,C,D,E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
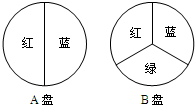 用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?请你并说明理由.
用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?请你并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com