
【题目】松立商店准备从永波机械厂购进甲、乙两种零件进行销售,若甲种零件的进价是乙种零件进价的![]() ,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件多4件.
,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件多4件.
(1)求每个甲种零件,每个乙种零件的进价分别为多少元?
(2)松立商店购进甲、乙两种零件共102个,准备将零件批发给零售商.甲种零件的批发价是100元,乙种零件的批发价是130元,松立商店计划从零售商处的获利超过2284元,通过计算求出松立商店最多给零售商批发多少个甲种零件?
【答案】(1)每个甲种零件的进价为80元,每个乙种零件的进价为100元;(2)松立商店最多给零售商批发77个甲种零件.
【解析】
(1)设乙零件进价为x元,则甲种零件的进价是![]() ,根据题意列出方程,解方程即可得到答案;
,根据题意列出方程,解方程即可得到答案;
(2)设最多给零售商批发m个甲种零件,则批发(102![]() m)个乙种零件,所得利润为w,则列出w与m的关系式,结合获利超过2284元,即可求出m的取值范围,即可得到答案.
m)个乙种零件,所得利润为w,则列出w与m的关系式,结合获利超过2284元,即可求出m的取值范围,即可得到答案.
解:(1)设乙零件进价为x元,则甲种零件的进价是![]() ,根据题意,
,根据题意,
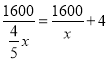 ,
,
解得:![]() ,
,
经检验,![]() 是原分式方程的解;
是原分式方程的解;
∴乙零件进价为100元,
∴甲种零件的进价是:![]() 元;
元;
(2)设最多给零售商批发m个甲种零件,则批发(102![]() m)个乙种零件,所得利润为w,
m)个乙种零件,所得利润为w,
∴![]() ,
,
∴![]() ;
;
∵松立商店计划从零售商处的获利超过2284元,
∴![]() ,
,
∴![]() ,
,
∵m为正整数,
∴m的最大正整数是77;
∴松立商店最多给零售商批发77个甲种零件.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】4月23日是世界读书日,设立的目的是推动更多的人去阅读和写作.为了解学生的课外阅读情况,对某校八年级1班“你最喜爱的课外阅读书目”进行调查(每名学生必须选一类且只能选一类阅读书目),并根据调查结果绘制成如图所示的两幅统计图(不完整).
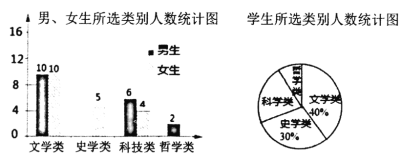
根据以上信息解决下列问题
(1)所抽查的学生中,选史学类的男生有______人,选哲学类的女生有______人;
(2)扇形统计图中“科学类”所对应扇形圆心角度数为_______°;
(3)若该校有2000名学生,请估计该校喜爱“科学类”的学生共有多少人?
(4)从所抽取的选“哲学类”的学生中,随机选取两名学生参加区级辩论赛,请用树状图或列表法求出所选取的两名学生恰好选中一个男生、一个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
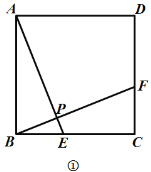
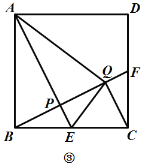
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图①,判断![]() 和
和![]() 之间的数量关系和位置关系,并证明;
之间的数量关系和位置关系,并证明;
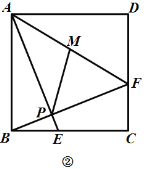
(2)如图②,连接![]() ,点
,点![]() 是
是![]() 中点,若
中点,若![]() ,
,![]() ,求线段
,求线段![]() 的长度;
的长度;
(3)如图③,作![]() 于点
于点![]() ,若
,若![]() ,求证:点
,求证:点![]() 是
是![]() 中点.
中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“半日走遍江淮大地,安徽风景尽在徽园”,位于省会合肥的徽园景点某年三月共接待游客![]() 万人,四月比三月旅游人数增加了
万人,四月比三月旅游人数增加了![]() ,五月比四月游客人数增加了
,五月比四月游客人数增加了![]() ,已知三月至五月徽园的游客人数平均月增长率为
,已知三月至五月徽园的游客人数平均月增长率为![]() ,则可列方程为( )
,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在环形跑道上同起点、同终点、同方向匀速跑步400米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离![]() (单位:
(单位:![]() )与乙出发的时间
)与乙出发的时间![]() (单位:
(单位:![]() )之间的关系如图所示,下列说法:①甲的速度为
)之间的关系如图所示,下列说法:①甲的速度为![]() ;②乙的速度为
;②乙的速度为![]() ;③乙出发
;③乙出发![]() 时甲、乙两人之间的距离为
时甲、乙两人之间的距离为![]() ;④甲到达终点时乙在终点休息了
;④甲到达终点时乙在终点休息了![]() ;⑤
;⑤![]() ,其中的正确的个数有( )
,其中的正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角形纸片![]() 和
和![]() 按图1所示放置,直角顶点重合在点
按图1所示放置,直角顶点重合在点![]() 处,
处,![]() ,
,![]() .保持纸片
.保持纸片![]() 不动,将纸片
不动,将纸片![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]()
![]() .当
.当![]() 与
与![]() 在同一直线上(如图2)时,
在同一直线上(如图2)时,![]() 的正切值等于_________.
的正切值等于_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于两个点
中,对于两个点![]() ,
,![]() 和图形
和图形![]() ,如果在图形上存在点
,如果在图形上存在点![]() ,
,![]() (
(![]() ,
,![]() 可以重合),使得
可以重合),使得![]() ,那么称点
,那么称点![]() 与点
与点![]() 是图形
是图形![]() 的一对“倍点”.已知⊙O的半径为
的一对“倍点”.已知⊙O的半径为![]() ,点
,点![]() .
.
(1)①点![]() 到⊙O的最大值是_______,最小值是_______;
到⊙O的最大值是_______,最小值是_______;
②在![]() ,
,![]() ,这两个点中,与点
,这两个点中,与点![]() 是⊙O的一对“倍点”的是_______;
是⊙O的一对“倍点”的是_______;
(2)在直线![]() 上存在点
上存在点![]() 与点
与点![]() 是⊙O的一对“倍点”,求
是⊙O的一对“倍点”,求![]() 的取值范围;
的取值范围;
(3)已知直线![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点的
轴分别交于点的![]() ,
,![]() ,若线段
,若线段![]() (含端点
(含端点![]() ,
,![]() )上所有点与点
)上所有点与点![]() 都是⊙O的一对“倍点”,直接写出
都是⊙O的一对“倍点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
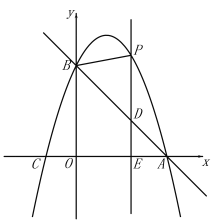
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过A,B.
经过A,B.
(1)求抛物线解析式;
(2)E(m,0)是x轴上一动点,过点E作![]() 轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
①点E在线段OA上运动,若△PBD是等腰三角形时,求点E的坐标;
②点E在x轴的正半轴上运动,若![]() ,请直接写出m的值.
,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
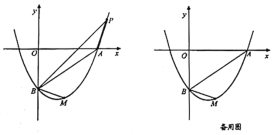
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com