

分析 (1)判断出△PBQ∽△DBC得出比例式建立方程即可得出结论;
(2)先判断出△BPM∽△BCD得出比例式求出PM=6-$\frac{3}{4}$t,BM=10-$\frac{5}{4}$t,再判断出△ADM∽△PBQ,得出比例式建立方程即可得出结论;
(3)分两种情况利用等腰三角形的性质即可得出结论.
解答 解:(1)在矩形ABCD中,AB=CD=6,BC=8,
∴∠C=90°,BD=10,
根据题意得,CP=BQ=t,BP=8-t,
∵PQ⊥BD,
∴∠BQP=90°,
∴∠BQP=∠C,
∵∠PBQ=∠DBC=45°,
∴△PBQ∽△DBC,
∴$\frac{BQ}{BC}=\frac{BP}{BD}$,
∴$\frac{t}{8}=\frac{8-t}{10}$,
∴t=$\frac{32}{9}$;
(2)∵PM⊥BC,∠C=90°,
∴PM∥CD,
∴△BPM∽△BCD,
∴$\frac{BP}{BC}=\frac{PM}{CD}=\frac{BM}{BD}$,
∴$\frac{8-t}{8}=\frac{PM}{6}=\frac{BM}{10}$,
∴PM=6-$\frac{3}{4}$t,BM=10-$\frac{5}{4}$t,
∴DM=$\frac{5}{4}$t,
∵PQ∥AM,
∴∠AMQ=∠MQP,
∴∠AMD=∠PQB,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADM=∠PBQ,
∴△ADM∽△PBQ,
∴$\frac{BQ}{DM}=\frac{BP}{AD}$,
∴$\frac{t}{\frac{5}{4}t}=\frac{8-t}{8}$,
∴t=$\frac{8}{5}$;
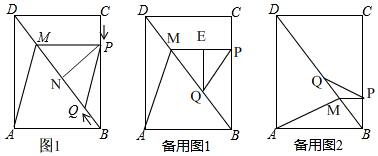
(3)
①当点Q在线段BM上时,
Ⅰ、若PM=MQ,
∴6-$\frac{3}{4}$t=10-$\frac{9}{4}$t,
∴t=$\frac{8}{3}$,
Ⅱ、若PM=PQ时,如图1,作PN⊥MQ于N,
∴∠PNM=90°,MN=$\frac{1}{2}$MQ=$\frac{1}{2}$(10-$\frac{9}{4}$t)=5-$\frac{9}{8}$t,
∴∠PNM=∠C,
∵PM∥CD,
∴∠PMQ=∠BDC,
∴△PMN∽△BDC,
∴$\frac{PM}{BD}=\frac{MN}{CD}$,
∴$\frac{6-\frac{3}{4}t}{10}=\frac{5-\frac{9}{8}t}{6}$,
∴t=$\frac{56}{27}$,
Ⅲ、若MQ=PQ时,如备用图1,作QE⊥PM于E,
∴QE∥BP,ME=$\frac{1}{2}$PM,
∴△QEM∽△BPM,
∴$\frac{ME}{MP}=\frac{MQ}{MB}=\frac{1}{2}$,
∴MQ=BQ,
∴10-$\frac{9}{4}$t=t,
∴t=$\frac{40}{13}$,
②当点M在线段BQ上时,如备用图2,∠PMQ是钝角,
∴只可能PM=QM,
∴6-$\frac{3}{4}$t=t-(10-$\frac{5}{4}$t),
∴t=$\frac{16}{3}$,
即:满足条件的时间t为$\frac{8}{3}$或$\frac{56}{27}$或$\frac{40}{13}$或$\frac{16}{3}$.
点评 此题是四边形综合题,主要考查了矩形的性质,相似三角形的判断和性质,等腰三角形的性质,解(1)的关键是判断出△PBQ∽△DBC,解(2)的关键是表示出PM=6-$\frac{3}{4}$t,BM=10-$\frac{5}{4}$t,解(3)的关键是分类讨论的思想解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
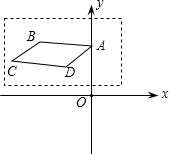 在如图所示的平面直角坐标系内,画在透明胶片上分平行四边形ABCD,点A的坐标是(0,2),现在将这张胶片先向右平移5个单位,再向下平移3个单位平移,使点A落在点A′处,则点A′的坐标为(5,-1).
在如图所示的平面直角坐标系内,画在透明胶片上分平行四边形ABCD,点A的坐标是(0,2),现在将这张胶片先向右平移5个单位,再向下平移3个单位平移,使点A落在点A′处,则点A′的坐标为(5,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 利用图中的网格线(最小的正方形的边长为1)画图;
利用图中的网格线(最小的正方形的边长为1)画图;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
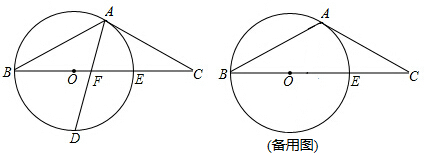
 已知将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF.
已知将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com