
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,过点(0,1)和(﹣1,0),给出以下结论:①ab<0;②4a+c<1+b2;③0<c+b+a<2;④0<b<2;⑤当x>﹣1时,y>0;⑥8a+7b+2c﹣9<0其中正确结论的个数是( )
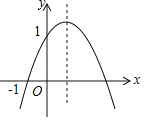
A.6B.5C.4D.3
【答案】C
【解析】
由开口方向及对称轴位置可判断①;由c=1且抛物线与x轴有两个交点,即b2﹣4ac>0可得b2﹣4a>c﹣1,即可判断②;由抛物线过(﹣1,0)且c=1得a﹣b+c=0即b=a+1>0,继而可得﹣1<a<0即0<a+1<1,最后由a+b+c=a+a+1+1=2a+2=2(a+1)可判断③;由b=a+1且0<a+1<1可判断④;由函数图象知当x>﹣1时,图象有位于x轴上方也有位于x轴下方的,即可判断⑤;由8a+7b+2c﹣9=8a+7(a+1)+2﹣9=15a且a<0可判断⑥.
解:∵开口向下且对称轴位于y轴右侧,
∴a<0,b>0,
∴ab<0,故①正确;
∵抛物线与x轴有两个交点且过点(0,1),
∴b2﹣4ac>0,c=1,
∴b2﹣4a>c﹣1,即4a+c<1+b2,故②正确;
∵抛物线过(﹣1,0),c=1,
∴a﹣b+c=0,
∴b=a+1>0,
∴﹣1<a<0,
∴0<a+1<1
又a+b+c=a+a+1+1=2a+2=2(a+1),且0<2(a+1)<2,
∴0<c+b+a<2,故③正确;
由③知,0<b=a+1<1,故④错误;
由函数图象知当x>﹣1时,y>0或y<0,故⑤错误;
∵8a+7b+2c﹣9=8a+7(a+1)+2﹣9=15a,且a<0,
∴8a+7b+2c﹣9<0,故⑥正确;
综上,正确的结论有①②③⑥共4个,
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A顺时针旋转θ(0°≤θ≤360°),得到矩形AEFG.

(1)当点E在BD上时,求证:AF∥BD;
(2)当GC=GB时,求θ;
(3)当AB=10,BG=BC=13时,求点G到直线CD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,直线y=kx﹣2k(k<0)的与y轴交于点A,与x轴交于点B.

(1)如图1,求点B的坐标;
(2)如图2,第一象限内的点C在经过B点的直线y=-![]() x+b上,CD⊥y轴于点D,连接BD,若S△ABD=2k+2,求C点的坐标(用含k的式子表示);
x+b上,CD⊥y轴于点D,连接BD,若S△ABD=2k+2,求C点的坐标(用含k的式子表示);
(3)如图3,在(2)的条件下,连接OC,交直线AB于点E,若3∠ABD﹣∠BCO=45°,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
(1)求证:直线DF与⊙O相切;
(2)求证:BF=EF;

查看答案和解析>>
科目:初中数学 来源: 题型:
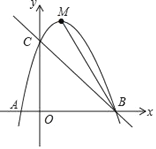
【题目】如图,在平面直角坐标系中.直线y=﹣x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+c经过B,C两点,与x轴负半轴交于点A,连结AC,A(-1,0)
(1)求抛物线的解析式;
(2)点P(m,n)是抛物线上在第一象限内的一点,求四边形OCPB面积S关于m的函数表达式及S的最大值;
(3)若M为抛物线的顶点,点Q在直线BC上,点N在直线BM上,Q,M,N三点构成以MN为底边的等腰直角三角形,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
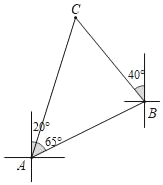
【题目】如图,一艘船由A港沿北偏东65°方向航行90![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,求A,C两港之间的距离.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,求A,C两港之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小琴和小江参加学校举行的“经典诵读"比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母![]() 依次表示这三个诵读材料),将
依次表示这三个诵读材料),将![]() 这三个字母分别写在
这三个字母分别写在![]() 张完全相同的不透明卡片的正面上,把这
张完全相同的不透明卡片的正面上,把这![]() 张卡片背面朝上洗匀后放在桌面上,比赛时小琴先从中随机抽取一张卡片, 记录下卡精上的内容,放回后洗匀,再由小江从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
张卡片背面朝上洗匀后放在桌面上,比赛时小琴先从中随机抽取一张卡片, 记录下卡精上的内容,放回后洗匀,再由小江从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
![]() 小琴诵读《论语》的概率是 .
小琴诵读《论语》的概率是 .
![]() 请用列表法或画树状图(树形图)法求小琴和小江诵读两个不同材料的概率.
请用列表法或画树状图(树形图)法求小琴和小江诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
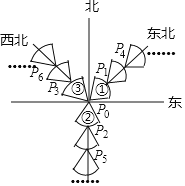
【题目】如图:图象①②③均是以P0为圆心,1个单位长度为半径的扇形,将图形①②③分别沿东北,正南,西北方向同时平移,每次移动一个单位长度,第一次移动后图形①②③的圆心依次为P1P2P3,第二次移动后图形①②③的圆心依次为P4P5P6…,依此规律,P0P2018=_____个单位长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com