
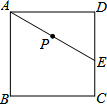
 如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于60°或120°.
如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于60°或120°. 分析 画出符合的两种情况,过N作NF⊥AD于F,根据HL证出Rt△MFN≌Rt△EDA,即可求出答案.
解答 解:分为两种情况:①如图1,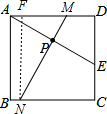
过N作NF⊥AD于F,
则∠NFA=∠MFN=90°,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠B=∠D=90°,
∴四边形AFNB是矩形,
∴NF=AB=AD,
∵∠NFM=∠D=90°,
在Rt△MFN和Rt△EDA中
$\left\{\begin{array}{l}{MN=A}\\{NF=AD}\end{array}\right.$
∴Rt△MFN≌Rt△EDA(HL),
∴∠AMN=∠AED,
∵∠DAE=30°,∠D=90°,
∴∠AMN=∠AED=180°-30°-90°=60°;
②如图2,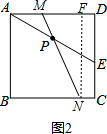
同法可求Rt△MFN≌Rt△EDA,
所以∠FMN=∠AED=60°,
所以∠AMN=180°-60°=120°.
故答案为:60°或120°
点评 本题考查了正方形的性质,全等三角形的性质和判定的应用,能求出符合的所有情况是解此题的关键,用了分类讨论思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
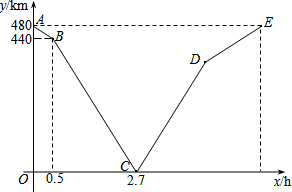 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决下列问题:
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 郑州市北环彩虹桥在上下班高峰期经常堵车,交通管理部门为了解交通拥堵情况,进行了统计分析,桥上的车流速度v(km/h)关于车流密度x(辆/km)的函数图象如图所示.
郑州市北环彩虹桥在上下班高峰期经常堵车,交通管理部门为了解交通拥堵情况,进行了统计分析,桥上的车流速度v(km/h)关于车流密度x(辆/km)的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.
如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}+1}{2}$ | B. | $\frac{3xy}{π}$ | C. | $\frac{3}{xy}$ | D. | $\frac{m-n}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com