
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=6cm£¬BC=8cm£¬µćP“ÓA³ö·¢ŃŲACĻņCµćŅŌ1ĄåĆ×/ĆėµÄĖŁ¶ČŌČĖŁŅĘ¶Æ£»µćQ“ÓC³ö·¢ŃŲCBĻņBµćŅŌ2ĄåĆ×/ĆėµÄĖŁ¶ČŌČĖŁŅĘ¶Æ£®µćP”¢Q·Ö±š“ÓĘšµćĶ¬Ź±³ö·¢£¬ŅĘ¶Æµ½Ä³Ņ»Ī»ÖĆŹ±ĖłŠčŹ±¼äĪŖtĆė£®

£Ø1£©µ±t=2Ź±£¬ĒóĻ߶ĪPQµÄ³¤¶Č£»
£Ø2£©µ±tĪŖŗĪÖµŹ±£¬”÷PCQµÄĆ껿µČÓŚ5cm2£æ
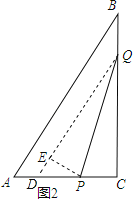
£Ø3£©ŌŚP”¢QŌĖ¶Æ¹ż³ĢÖŠ£¬ŌŚÄ³Ņ»Ź±æĢ£¬Čō½«”÷PQC·ÕŪ£¬µĆµ½”÷EPQ£¬ČēĶ¼2£¬PEÓėABÄÜ·ń“¹Ö±£æČōÄÜ£¬Ēó³öĻąÓ¦µÄtÖµ£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©![]() ĄåĆ×£»£Ø2£©µ±t=1ĆėŹ±£¬”÷PCQµÄĆ껿µČÓŚ5cm2£»£Ø3£©µ±t=
ĄåĆ×£»£Ø2£©µ±t=1ĆėŹ±£¬”÷PCQµÄĆ껿µČÓŚ5cm2£»£Ø3£©µ±t=![]() Ź±£¬PE”ĶAB£®
Ź±£¬PE”ĶAB£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©µ±t=2Ź±£¬æÉĒó³öCP£¬CQµÄ³¤£¬øł¾Ż¹“¹É¶ØĄķ¼“æÉĒó³öĻ߶Ī¼“Š±±ßPQµÄ³¤£»
£Ø2£©ÓÉČż½ĒŠĪĆ껿¹«Ź½æɽØĮ¢¹ŲÓŚtµÄ·½³Ģ£¬½ā·½³ĢĒó³ötµÄÖµ¼“æÉ£»
£Ø3£©ŃÓ³¤QE½»ACÓŚµćD£¬ČōPE”ĶAB£¬ŌņQD”ĪAB£¬ĖłŅŌæɵƔ÷CQD”×”÷CBA£¬ÓÉĻąĖĘČż½ĒŠĪµÄŠŌÖŹ£ŗ¶ŌÓ¦±ßµÄ±ČÖµĻąµČæÉĒó³öDE=0.5t£¬Ņ×Ö¤”÷ABC”×”÷DPE£¬ŌŁÓÉĻąĖĘČż½ĒŠĪµÄŠŌÖŹæɵĆ![]() £¬°ŃŅŃÖŖŹż¾Ż“śČė¼“æÉĒó³ötµÄÖµ£®
£¬°ŃŅŃÖŖŹż¾Ż“śČė¼“æÉĒó³ötµÄÖµ£®
½ā£ŗ£Ø1£©µ±t=2Ź±£¬
”ßµćP“ÓA³ö·¢ŃŲACĻņCµćŅŌ1ĄåĆ×/ĆėµÄĖŁ¶ČŌČĖŁŅĘ¶Æ£»µćQ“ÓC³ö·¢ŃŲCBĻņBµćŅŌ2ĄåĆ×/ĆėµÄĖŁ¶ČŌČĖŁŅĘ¶Æ£¬
”ąAP=2ĄåĆ×£¬QC=4ĄåĆ×£¬
”ąPC=4£¬ŌŚRt”÷PQCÖŠPQ=![]() =
=![]() ĄåĆ×£»
ĄåĆ×£»
£Ø2£©”ßµćP“ÓA³ö·¢ŃŲACĻņCµćŅŌ1ĄåĆ×/ĆėµÄĖŁ¶ČŌČĖŁŅĘ¶Æ£»µćQ“ÓC³ö·¢ŃŲCBĻņBµćŅŌ2ĄåĆ×/ĆėµÄĖŁ¶ČŌČĖŁŅĘ¶Æ£¬
”ąPC=AC©AP=6©t£¬CQ=2t£¬
”ąS”÷CPQ=![]() CPCQ=
CPCQ=![]() £¬
£¬
”ąt2©6t+5=0
½āµĆt1=1£¬t2=5£Ø²»ŗĻĢāŅā£¬ÉįČ„£©
”ąµ±t=1ĆėŹ±£¬”÷PCQµÄĆ껿µČÓŚ5cm2£»
£Ø3£©ÄÜ“¹Ö±£¬ĄķÓÉČēĻĀ£ŗ
ŃÓ³¤QE½»ACÓŚµćD£¬
”ß½«”÷PQC·ÕŪ£¬µĆµ½”÷EPQ£¬
”ą”÷QCP”Õ”÷QEP£¬
”ą”ĻC=”ĻQEP=90”ć£¬
ČōPE”ĶAB£¬ŌņQD”ĪAB£¬
”ą”÷CQD”×”÷CBA£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ąQD=2.5t£¬
ӧQC=QE=2t
”ąDE=0.5t
Ņ×Ö¤”÷ABC”×”÷DPE£¬
”ą![]()
”ą![]() £¬
£¬
½āµĆ£ŗt=![]() £Ø0”Üt”Ü4£©£¬
£Ø0”Üt”Ü4£©£¬
×ŪÉĻæÉÖŖ£ŗµ±t=![]() Ź±£¬PE”ĶAB£®
Ź±£¬PE”ĶAB£®


 æĪĒ°æĪŗóĶ¬²½Į·Ļ°ĻµĮŠ“š°ø
æĪĒ°æĪŗóĶ¬²½Į·Ļ°ĻµĮŠ“š°ø æĪĢĆŠ”×÷ŅµĻµĮŠ“š°ø
æĪĢĆŠ”×÷ŅµĻµĮŠ“š°ø »ĘøŌŠ”דŌŖæŚĖćĖŁĖćĮ·Ļ°²įĻµĮŠ“š°ø
»ĘøŌŠ”דŌŖæŚĖćĖŁĖćĮ·Ļ°²įĻµĮŠ“š°ø ³É¹¦ŃµĮ·¼Ę»®ĻµĮŠ“š°ø
³É¹¦ŃµĮ·¼Ę»®ĻµĮŠ“š°ø ±¶ĖŁŃµĮ··ØÖ±ĶØÖŠæ¼æ¼µćĻµĮŠ“š°ø
±¶ĖŁŃµĮ··ØÖ±ĶØÖŠæ¼æ¼µćĻµĮŠ“š°ø Ņ»¾ķøć¶ØĻµĮŠ“š°ø
Ņ»¾ķøć¶ØĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖaŹĒĮ½Ī»Źż£¬bŹĒŅ»Ī»Źż£¬°Ńa½ÓŠ“ŌŚbµÄŗóĆę£¬¾Ķ³ÉĪŖŅ»øöČżĪ»Źż.ÕāøöČżĪ»ŹżæɱķŹ¾³É£Ø £©
A.10b+a
B.ba
C.100b+a
D.b+10a
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČż½ĒŠĪĮ½±ßµÄ³¤·Ö±šŹĒ8ŗĶ6£¬µŚ3±ßµÄ³¤ŹĒŅ»ŌŖ¶ž“Ī·½³Ģx2©16x+60=0µÄŅ»øöŹµŹżøł£¬ŌņøĆČż½ĒŠĪµÄĆ껿ŹĒ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢĘ·¼ŪøńaŌŖ£¬½µ¼Ū10%ŗóÓÖ½µ¼Ū10%£¬ĻśŹŪ¶īĆĶŌö£¬ÉĢµź¾ö¶ØŌŁĢį¼Ū20%£¬Ģį¼ŪŗóÕāÖÖ²śĘ·¼ŪøńĪŖ£Ø £©
A.aŌŖ
B.1.08aŌŖ
C.0.972aŌŖ
D.0.96aŌŖ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ
![]()
£Ø1£©ĢīæÕ£ŗAB= £¬BC= £»
£Ø2£©ČōµćAŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ×óŌĖ¶Æ£¬Ķ¬Ź±£¬µćBŗĶµćC·Ö±šŅŌĆæĆė3øöµ„Ī»³¤¶ČŗĶ7øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÓŅŌĖ¶Æ£®ŹŌĢ½Ė÷£ŗBC©ABµÄÖµŹĒ·ńĖę×ÅŹ±¼äµÄ±ä»Æ¶ųøıä£æĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄ·½³Ģmx2©£Øm+2£©x+2=0£Øm”Ł0£©£®
£Ø1£©ĒóÖ¤£ŗ·½³Ģ×ÜÓŠĮ½øöŹµŹżøł£»
£Ø2£©Čō·½³ĢµÄĮ½øöŹµŹżøł¶¼ŹĒÕūŹż£¬ĒóÕżÕūŹżmµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCµÄÄŚ½Ē”ĻABCÓėĶā½Ē”ĻACDµÄĘ½·ÖĻß½»ÓŚµćE£¬ĒŅCE”ĪAB£¬ACÓėBE½»ÓŚµćE£¬ŌņĻĀĮŠ½įĀŪ“ķĪóµÄŹĒ£Ø £©

A£®CB=CE B£®”ĻA=”ĻECD C£®”ĻA=2”ĻE D£®AB=BF
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµćP£Ø3£¬1£©¹ŲÓŚxÖįµÄ¶Ō³ĘµćP”äµÄ×ų±źŹĒ_________.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĆęµÄ·½øńĶ¼ŹĒÓɱ߳¤ĪŖ1µÄČōøÉøöŠ”Õż·½ŠĪĘ“³ÉµÄ£¬ABCµÄ¶„µćA£¬B£¬C¾łŌŚŠ”Õż·½ŠĪµÄ¶„µćÉĻ£®
£Ø1£©ŌŚĶ¼ÖŠ½ØĮ¢Ē”µ±µÄĘ½ĆęÖ±½Ē×ų±źĻµ£¬Č”Š”Õż·½ŠĪµÄ±ß³¤ĪŖŅ»øöµ„Ī»³¤¶Č£¬ĒŅŹ¹µćAµÄ×ų±źĪŖ£Ø©4£¬2£©£»
£Ø2£©ŌŚ£Ø1£©ÖŠ½ØĮ¢µÄĘ½ĆęÖ±½Ē×ų±źĻµÄŚ»³ö”÷ABC¹ŲÓŚyÖį¶Ō³ĘµÄ”÷A1B1C1£¬²¢Š“³ö”÷A1B1C1ø÷¶„µćµÄ×ų±ź£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com