
【题目】如图,点![]() 和点
和点![]() 在数轴上对应的数分别为
在数轴上对应的数分别为![]() 和
和![]() ,且
,且![]() .
.
(1)线段![]() 的长为 ;
的长为 ;
(2)点![]() 在数轴上所对应的数为
在数轴上所对应的数为![]() ,且
,且![]() 是方程
是方程![]() 的解,在线段
的解,在线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() ?若存在,请求出点
?若存在,请求出点![]() 在数轴上所对应的数,若不存在,请说明理由;
在数轴上所对应的数,若不存在,请说明理由;
(3)在(2)的条件下,线段![]() 和
和![]() 分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动,运动时间为
分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动,运动时间为![]() 秒,点
秒,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点,若
的中点,若![]() ,求
,求![]() 的值.
的值.
![]()
【答案】(1)10;(2)存在,点![]() 对应的数为2,见解析;(3)
对应的数为2,见解析;(3)![]() 的值为6
的值为6![]() 或16
或16![]()
【解析】
(1)根据题意求出![]() 和
和![]() 的值,进而即可求出线段
的值,进而即可求出线段![]() 的长;
的长;
(2)由题意先解出x,再根据题意求出点![]() 在数轴上所对应的数;
在数轴上所对应的数;
(3)根据题意先求出![]() 、
、![]() 初始位置对应数,再根据题意运动时间为
初始位置对应数,再根据题意运动时间为![]() 秒以及
秒以及![]() ,建立关系式,并求出t值即可.
,建立关系式,并求出t值即可.
解:(1)∵![]()
∴![]() ,
,
∵点![]() 和点
和点![]() 在数轴上对应的数分别为
在数轴上对应的数分别为![]() 和
和![]() ,
,
∴线段![]() 的长为
的长为![]() .
.
故答案为:10.
(2)∵![]()
解得,![]()
即点![]() 在数轴上对应的数为14.
在数轴上对应的数为14.
∵点![]() 在线段
在线段![]() 上.
上.
∴![]()
∵![]()
∴![]()
解得:![]()
∴14-12=2
即点![]() 对应的数为2.
对应的数为2.
(3)由题意知,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,
∴![]() 、
、![]() 初始位置对应数为0,11.
初始位置对应数为0,11.
![]() 对应的数是
对应的数是![]()
![]() 对应的数是
对应的数是 ![]()
又∵![]() 在
在![]() 上,
上, ![]() 在
在![]() 上,
上,
∴可知![]() 的速度在
的速度在![]() 处向右,速度为6个单位/秒,
处向右,速度为6个单位/秒, ![]() 的速度在11处向右速度为5个单位/秒,
的速度在11处向右速度为5个单位/秒,
运动![]() 秒后,
秒后,
![]() 对应的数为:
对应的数为:![]() ,
, ![]() 对应的数为:
对应的数为:![]() ,
,
∵![]()
∴![]()
解得,![]() 或16,
或16,
![]() 的值为6
的值为6![]() 或16
或16![]() .
.


科目:初中数学 来源: 题型:
【题目】今年我国和俄罗斯联合军事演习中,一核潜艇在海下时而上升,时而下降.核潜艇的初始位置在海平面下500米,下面是核潜艇在某段时间内运动情况(把上升记为“+”下降记为“﹣”,单位:米):﹣280,﹣50,40,30,﹣40,75,﹣55
(1)现在核潜艇处在什么位置(海平面下多少米)?
(2)假如核潜艇每上升或下降1米核动力装置所提供的能量相当于20升汽油燃烧所产生的能量,那么在这一时刻内核动力装置所提供的能量相当于多少升汽油燃烧所产生的能量?
查看答案和解析>>
科目:初中数学 来源: 题型:
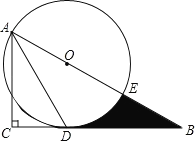
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送![]() 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位:![]() ):
):
第 | 第 | 第 | 第 | 第 |
|
|
|
|
|
(1)接送完第![]() 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油![]() 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过![]() 收费
收费![]() 元,超过
元,超过![]() 的部分按每千米
的部分按每千米![]() 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从锦江区社保局获悉,我区范围内已经实现了全员城乡居民新型社会合作医疗保险制度.享受医保的城乡居民可在规定的医院就医并按规定标准报销部分医疗费用.下表是住院费用报销的标准:
住院费用x(元) | 0<x<5000 | 5000<x≤20000 | x>20000 |
每年报销比例 | 40% | 50% | 60% |
(说明:住院费用的报销采取分段计算方式,如:某人一年住院费用共30000元,则5000元按40%报销,15000元按50%报销,余下的10000元按60%报销;实际支付的住院费=住院费用-按标准报销的金额.)
(1)若我区居民张大哥一年住院费用为20000元,则按标准报销的金额为 元,张大哥实际支付了 元的住院费;
(2)若我区居民王大爷一年内本人实际支付的住院费用为21000元,则王大爷当年的住院费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
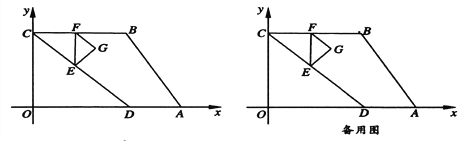
【题目】如图,四边形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半抽上,点
轴的正半抽上,点![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 的坐标为
的坐标为![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿线段
个单位长度的速度沿线段![]() 向点
向点![]() 运动,过点
运动,过点![]() 作
作![]() 的垂线
的垂线![]() 交线段
交线段![]() 于点
于点![]() ,以线段
,以线段![]() 为斜边向右作等腰直角
为斜边向右作等腰直角![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒(
秒(![]() ).
).
(1) 点F的坐标为( , )点![]() 的坐标为( , )(用含
的坐标为( , )(用含![]() 的代数式表示),
的代数式表示),
(2)连接![]() 、
、![]() ,当
,当![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)设点![]() 从点
从点![]() 出发时,点
出发时,点![]() 、
、![]() 、
、![]() 都与点
都与点![]() 重合,点
重合,点![]() 在运动过程中,当
在运动过程中,当![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 运动的时间
运动的时间![]() 的值﹒
的值﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了食品安全管理,有关部门对某大型超市的甲、乙两种品牌食用油共抽取18瓶进行检测,检测结果分成“优秀”“合格”和“不合格”三个等级,数据处理后制成以下折线统计图和扇形统计图.
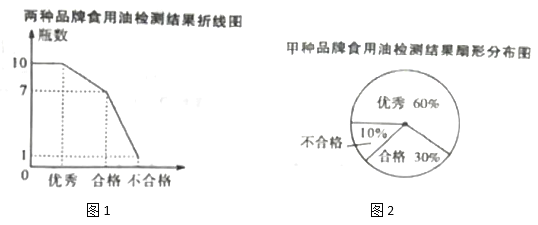
(1)甲、乙两种品牌的食用油各被抽取了多少瓶进行检测?
(2)乙品牌食用油“优秀”的瓶数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出P点的坐标,若不存在说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家文化用品商场平时以同样价格出售相同的商品.六一期间两家商场都让利酬宾,其中甲商场所有商品一律按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
(1)分别写出两家商场购物金额![]() (元)与商品原价
(元)与商品原价![]() (元)的函数解析式;
(元)的函数解析式;
(2)在如图所示的直角坐标系中画出(1)中函数的图象;
(3)六一期间如何选择这两家商场购物更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com