
【题目】在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
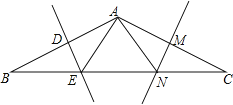
(1)求△AEN的周长;
(2)求证:BE=EN=NC.
【答案】(1)12;(2)见解析
【解析】试题分析:(1)根据线段的垂直平分线的性质得到EB=EA,NA=NC,根据三角形的周长公式计算即可;
(2)根据等腰三角形的性质和三角形的外角的性质证明△AEN是等边三角形,等量代换证明即可.
试题解析:(1)∵DE是AB的垂直平分线,
∴EB=EA,
∵MN是AC的垂直平分线,
∴NA=NC,
则△AEN的周长=AE+AN+EN=BE+EN+NC=BC=12;
(2)证明:∵AB=AC,∠B=30°,
∴∠C=∠B=30°,
∵EB=EA,NA=NC,
∴∠EAB=∠B=30°,∠NAC=∠C=30°,
∴∠AEN=∠EAB+∠B=60°,∠ANE=∠NAC+∠C=60°,
∴△AEN是等边三角形,
∴BE=EN=NC.


科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如图①,在△ABC中,试说明∠A+∠B+∠C=180°.
分析:通过画平行线,将∠A、∠B、∠C作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是A.B两所学校艺术节期间收到的各类艺术作品情况的统计图:


A学校 B学校
(1)从图中你能否看出哪所学校收到的水粉画作品的数量多?为什么?
(2)已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺木作品的总数分别是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(请用“画树状图”或“列表”等方法写出分析过程);
(2)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为 ![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE、BF、DC是直线,B在直线AC上,E在直线DF上,∠1=∠2,∠A=∠F.
求证:∠C=∠D.

证明:因为∠1=∠2(已知),∠1=∠3( )
得∠2=∠3( )
所以AE//_______( )
得∠4=∠F( )
因为__________(已知)
得∠4=∠A
所以______//_______( )
所以∠C=∠D( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
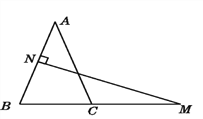
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是以O为圆心,AB为直径的半圆的中点,AB=2,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的斜边和直角边所在的直线与直径AB分别相交于C,D两点.设线段AD的长为x,线段BC的长为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?
【答案】小红每消耗1千卡能量需要行走30步.
【解析】分析:设小红每消耗1千卡能量需要行走x步,则小明每消耗1千卡能量需要行走(x+10)步,根据数量关系消耗能量千卡数=行走步数÷每消耗1千卡能量需要行走步数结合小明步行12000步与小红步行9000步消耗的能量相同,即可得出关于x的分式方程,解之后经检验即可得出结论.
详解:设小红每消耗1千卡能量需要行走x步,则小明每消耗1千卡能量需要行走(x+10)步,
根据题意,得
![]() ,
,
解得x=30.
经检验:x=30是原方程的解.
答:小红每消耗1千卡能量需要行走30步.
点睛:本题考查了分式方程的应用,根据数量关系消耗能量千卡数=行走步数÷每消耗1千卡能量需要行走步数列出关于x的分式方程是解题的关键.
【题型】解答题
【结束】
25
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于F,连接CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF为正方形,请你添加适当的条件并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com