
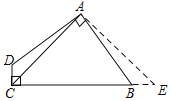
【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )

A. 15 B. 12.5 C. 14.5 D. 17
【答案】B
【解析】过A作AE⊥AC,交CB的延长线于E,判定△ACD≌△AEB,即可得到△ACE是等腰直角三角形,四边形ABCD的面积与△ACE的面积相等,根据S△ACE=![]() ×5×5=12.5,即可得出结论.
×5×5=12.5,即可得出结论.
如图,过A作AE⊥AC,交CB的延长线于E,
∵∠DAB=∠DCB=90°,
∴∠D+∠ABC=180°=∠ABE+∠ABC,
∴∠D=∠ABE,
又∵∠DAB=∠CAE=90°,
∴∠CAD=∠EAB,
又∵AD=AB,
∴△ACD≌△AEB,
∴AC=AE,即△ACE是等腰直角三角形,
∴四边形ABCD的面积与△ACE的面积相等,
∵S△ACE=![]() ×5×5=12.5,
×5×5=12.5,
∴四边形ABCD的面积为12.5,
故选B.


科目:初中数学 来源: 题型:
【题目】如图所示,三条公路两两相交,交点分别为A、B、C,现计划修一个油库,要求到三条公路的距离相等,可供选择的地址有( )

A. 一处 B. 二处 C. 三处 D. 四处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论,其中正确结论是( )
A.b2<4ac
B.2a+b=0
C.a+b+c>0
D.若点B( ![]() ,y1)、C(
,y1)、C( ![]() ,y2)为函数图象上的两点,则y1<y2
,y2)为函数图象上的两点,则y1<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,若点A(﹣1,y1)、B(﹣6,y2)是它图象上的两点,则y1与y2的大小关系是( )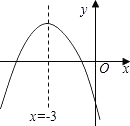
A.y1<y2
B.y1=y2
C.y1>y2
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有几个?
(1)AE平分∠DAB;(2)△EBA≌△DCE; (3)AB+CD=AD;(4)AE⊥DE;(5)AB//CD;
大家一起热烈地讨论交流,小红第一个得出正确答案,是( ).

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,将正方形的边AD绕点A顺时针旋转到AE,连接BE、DE,过点A作AF⊥BE于F,交直线DE于P.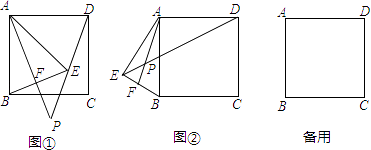
(1)如图①,若∠DAE=40°,求∠P的度数;
(2)如图②,若90°<∠DAE<180°,其它条件不变,试探究线段AP、DP、EP之间的数量关系,并说明理由;
(3)继续旋转线段AD,若旋转角180°<∠DAE<270°,则线段AP、DP、EP之间的数量关系为(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com