
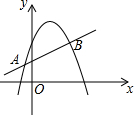
 如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.
如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4. 科目:初中数学 来源: 题型:填空题
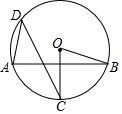 如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=35度.
如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=35度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
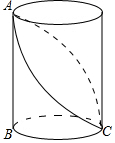 如图,已知圆柱的底面直径BC=$\frac{6}{π}$,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( )
如图,已知圆柱的底面直径BC=$\frac{6}{π}$,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( )| A. | $3\sqrt{2}$ | B. | $3\sqrt{5}$ | C. | $6\sqrt{5}$ | D. | $6\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )| A. | AB=AD | B. | BC=CD | C. | $\widehat{AB}=\widehat{AD}$ | D. | ∠BCA=∠DCA |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两人要测量灯塔AB的高度,甲在C处用高度为1.5米的侧角仪测得塔顶A的仰角为72°,乙在E处用高度为1.8米的测角仪测得塔顶A的仰角为50°,点B、C、E在同一条直线上,且甲乙两人的距离CE=10米,请你根据所测量的数据计算灯塔AB的高度.(结果精确到0.1m)(参考数据:sin50°≈$\frac{4}{5}$,cos50°≈$\frac{16}{25}$,tan50°≈$\frac{5}{4}$,sin72°≈$\frac{19}{20}$,cos72°≈$\frac{3}{10}$,tan72°≈$\frac{19}{6}$)
甲、乙两人要测量灯塔AB的高度,甲在C处用高度为1.5米的侧角仪测得塔顶A的仰角为72°,乙在E处用高度为1.8米的测角仪测得塔顶A的仰角为50°,点B、C、E在同一条直线上,且甲乙两人的距离CE=10米,请你根据所测量的数据计算灯塔AB的高度.(结果精确到0.1m)(参考数据:sin50°≈$\frac{4}{5}$,cos50°≈$\frac{16}{25}$,tan50°≈$\frac{5}{4}$,sin72°≈$\frac{19}{20}$,cos72°≈$\frac{3}{10}$,tan72°≈$\frac{19}{6}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
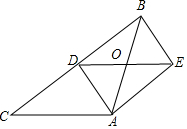
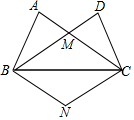 如图,在△ABC和△BCD中,AB=DC,AC=DB,AC、DB交于点M.
如图,在△ABC和△BCD中,AB=DC,AC=DB,AC、DB交于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com