
【题目】如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求![]() 的值;
的值;
(3)在(2)的条件下,若![]() =k(k为大于
=k(k为大于![]() 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示![]() 的值.
的值.

【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)证法一,利用菱形性质得AB=CD,AB∥CD,利用平行四边形的性质得AB=EF,AB∥EF,则CD=EF,CD∥EF,再根据平行线的性质得∠CDM=∠FEM,则可根据“AAS”判断△CDM≌△FEM,所以DM=EM;
证法二,利用菱形性质得DH=BH,利用平行四边形的性质得AF∥BE,再根据平行线分线段成比例定理得到![]() =1,所以DM=EM;
=1,所以DM=EM;
(2)由△CDM≌△FEM得到CM=FM,设AD=a,CM=b,则FM=b,EF=AB=a,再证明四边形ABCD为正方形得到AC=![]() a,接着证明△ANF为等腰直角三角形得到NF=a+
a,接着证明△ANF为等腰直角三角形得到NF=a+![]() b,则NE=NF+EF=2a+
b,则NE=NF+EF=2a+![]() b,然后计算
b,然后计算![]() 的值;
的值;
(3)由于![]() =
=![]() =
=![]() =k,则
=k,则![]() =
=![]() ,然后表示出
,然后表示出![]() =
=![]() =
=![]() ,再把
,再把![]() =
=![]() 代入计算即可.
代入计算即可.
试题解析:解:(1)如图1,证法一:∵四边形ABCD为菱形,∴AB=CD,AB∥CD,∵四边形ABEF为平行四边形,∴AB=EF,AB∥EF,∴CD=EF,CD∥EF,∴∠CDM=∠FEM,在△CDM和△FEM中,∵∠CMD=∠FME,∠CDM=∠FEM,CD=EF,∴△CDM≌△FEM,∴DM=EM,即点M是DE的中点;
证法二:∵四边形ABCD为菱形,∴DH=BH,∵四边形ABEF为平行四边形,∴AF∥BE,∵HM∥BE,∴ ![]() =1,∴DM=EM,即点M是DE的中点;
=1,∴DM=EM,即点M是DE的中点;
(2)∵△CDM≌△FEM,∴CM=FM,设AD=a,CM=b,∵∠ABE=135°,∴∠BAF=45°,∵四边形ABCD为菱形,∴∠NAF=45°,∴四边形ABCD为正方形,∴AC=![]() AD=
AD=![]() a,∵AB∥EF,∴∠AFN=∠BAF=45°,∴△ANF为等腰直角三角形,∴NF=
a,∵AB∥EF,∴∠AFN=∠BAF=45°,∴△ANF为等腰直角三角形,∴NF=![]() AF=
AF=![]() (
(![]() a+b+b)=a+
a+b+b)=a+![]() b,∴NE=NF+EF=a+
b,∴NE=NF+EF=a+![]() b+a=2a+
b+a=2a+![]() b,∴
b,∴![]() =
=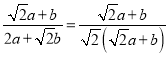 =
=![]() ;
;
(3)∵![]() =
=![]() =
=![]() =k,∴
=k,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?

(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大源村在“山上再造一个通城”工作中,计划植树200亩,全村在完成植树40亩后,党的群众路线教育实践活动工作小组加入村民植树活动,并且该活动小组植树的速度是全村植树速度的1.5倍,整个植树过程共用了13天完成.
(1)全村每天植树多少亩?
(2)如果全村植树每天需2000元工钱,党的群众路线教育实践活动工作小组是义务植树,因此实际工钱比计划节约多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1,
(x﹣1)(x2+x+1)=x3﹣1,
(x﹣1)(x3+x2+x+1)=x4﹣1,
……
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= .
(2)你能否由此归纳出一般性规律:(x﹣1)(xn+xn﹣1+…+x+1)= .
(3)根据以上规律求1+3+32+…+334+335的结果
查看答案和解析>>
科目:初中数学 来源: 题型:
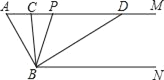
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com