
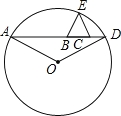
【题目】如图,A,B,C,D为一直线上4个点,BC=3,△BCE为等边三角形,⊙O过A,D,E三点,且∠AOD=120°,设AB=x,CD=y,则y与x的函数关系式是( )
A.y=![]() B.y=
B.y=![]() xC.y=3x+3D.y=
xC.y=3x+3D.y=![]()
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:

b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学小组的两位同学准备测量两幢教学楼之间的距离,如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15m,CD=20m,求两幢教学楼之间的距离BD.
(结果精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点,过点
是抛物线的顶点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
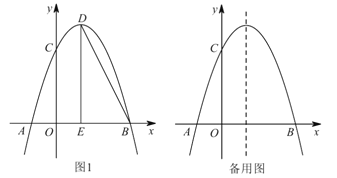
(1)求此抛物线的解析式;
(2)点![]() 是抛物线上的动点,设点
是抛物线上的动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②过点![]() 作
作![]() 轴,与抛物线交于点
轴,与抛物线交于点![]() ,
,![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]() ,
,![]() ,将
,将![]() 沿着
沿着![]() 翻折,得
翻折,得![]() ,若四边形
,若四边形![]() 恰好为正方形,直接写出
恰好为正方形,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
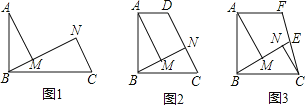
【题目】如图1,AB⊥BC,分别过点A,C作BM的垂线,垂足分别为M,N.
(1)求证:BMBC=ABCN;
(2)若AB=BC.
①如图2,若BM=MN,过点A作AD∥BC交CM的延长线于点D,求DN:CN的值;
②如图3,若BM>MN,延长BN至点E,使BM=ME,过点A作AF∥BC交CE的延长线于点F,若E是CF的中点,且CN=1,直接写出线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
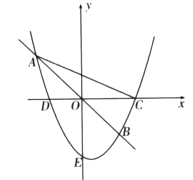
【题目】定义:若抛物线![]() 上有两点
上有两点![]() 关于原点对称(点A在点B左侧)则称它为“完美抛物线”,如图.
关于原点对称(点A在点B左侧)则称它为“完美抛物线”,如图.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若抛物线![]() 是“完美抛物线”,求
是“完美抛物线”,求![]() 的值;
的值;
(3)若完美抛物线![]() 与
与![]() 轴交于点E与
轴交于点E与![]() 轴交于
轴交于![]() 两点(点D在点C的左侧),顶点为点
两点(点D在点C的左侧),顶点为点![]() ,
,![]() 是以
是以![]() 为直角边的直角三角形,点
为直角边的直角三角形,点![]() ,求点
,求点![]() 中
中![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
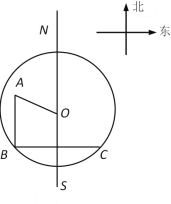
【题目】机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.(本题参考数据:sin67.4°=![]() ,cos67.4°=
,cos67.4°=![]() ,tan67.4°=
,tan67.4°=![]() )
)
(1)求弦BC的长;
(2)请判断点A和圆的位置关系,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com