
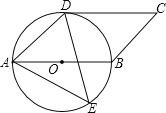
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
【答案】(1)CD与圆O相切;(2)AE=5.
【解析】
(1)连接OD,则∠AOD=为直角,由四边形ABCD是平行四边形,则AB∥CD,从而得出∠CDO=90°,即可证出答案;
(2)连接BE,则∠ADE=∠ABE,根据题意得sin∠ABE=![]() . 由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
. 由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
解:(1)CD与圆O相切. 证明:连接OD,则∠AOD=2∠AED =2×450=900
∵四边形ABCD是平行四边形,∴AB//DC
∴∠CDO=∠AOD=90°
∴OD⊥CD
∴CD与圆O相切
(2)连接BE,则∠ADE=∠ABE
∴sin∠ADE=sin∠ABE=![]()
∵AB是圆O的直径,∴∠AEB=900,AB=2×3=6
在Rt△ABE中,sin∠ABE=![]() .
.
∴AE=5 .


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
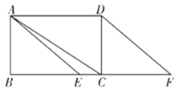
【题目】如图,在矩形![]() 中,点
中,点![]() 是边
是边![]() 上一点(不与点
上一点(不与点![]() 重合),点
重合),点![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() .
.
(1)求证:![]()
(2)连接![]() ,其中
,其中![]()
①当四边形![]() 是菱形时,求线段
是菱形时,求线段![]() 与线段
与线段![]() 之间的距离;
之间的距离;
②若点![]() 是
是![]() 的内心,连接
的内心,连接![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点.
AC,E是AC的中点.

(1)求证:四边形BDEC是平行四边形;
(2)连接AD、BE,△ABC添加一个条件: ,使四边形DBEA是矩形(不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2均是![]() 的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点
的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点![]() 、
、![]() 、
、![]() 、
、![]() 均在格点上.在图1、图2中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
均在格点上.在图1、图2中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
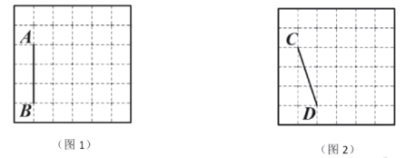
(1)在图1中以线段![]() 为边画一个
为边画一个![]() ,使
,使![]() ,且
,且![]() 的面积为3;
的面积为3;
(2)在图2中以线段![]() 为边画一个四边形
为边画一个四边形![]() ,使四边形
,使四边形![]() 既是轴对称图形又是中心对称图形;
既是轴对称图形又是中心对称图形;
(3)直接写出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
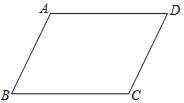
【题目】如图,已知四边形ABCD是平行四边形,AB<AD.
(1)利用尺规作图作出∠ABC的角平分线BG,交AD于点E,记点A关于BE对称点为F(要求保留作图痕迹,不写作法);
(2)在(1)所作的图中,若AF=6,AB=5,求BE的长和四边形ABFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图l、图2均为8×6的方格纸(每个小正方形的边长均为1),在方格纸中各有一条线段AB,其中点A、B均在小正方形的顶点上,请按要求画图:

(1)在图l中画一直角△ABC,使得tan∠BAC=![]() ,点C在小正方形的顶点上;
,点C在小正方形的顶点上;
(2)在图2中画一个□ABEF,使得□ABEF的面积为图1中△ABC面积的4倍,点E、F在小正方形的顶点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
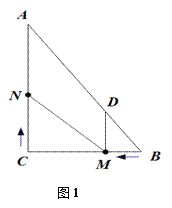
【题目】如图1,在Rt△ABC中,∠C=90,BC=6,AC=8.动点M从点B开始沿边BC向点C以每秒1个单位长度的速度运动,动点N从点C开始沿边CA向点A以每秒2个单位长度的速度运动,点M、N同时出发,且当其中一点到达端点时,另一点也随之停止运动.过点M作MD∥AC,交AB于点D,连接MN.设运动时间为t秒(t≥0).
(1)当t为何值时,四边形ADMN为平行四边形?
(2)是否存在t的值,使四边形ADMN为菱形?若存在,求出t的值;若不存在,说明理由.并探究只改变点N的速度(匀速运动),使四边形ADMN在某一时刻为菱形,求点N的速度;
(3)如图2,在整个运动过程中,求出线段MN中点P所经过的路径长.
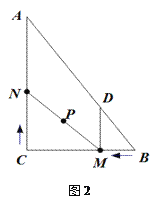
查看答案和解析>>
科目:初中数学 来源: 题型:
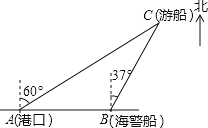
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,
的弦,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
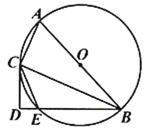
(1)![]() ________
________![]() (填“>”,“<”或“=”);
(填“>”,“<”或“=”);
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() 的直径为10,sin∠BAC=
的直径为10,sin∠BAC=![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com