
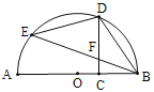
【题目】如图,AB是⊙O的直径,C是线段OB上的一点(不与点B重合),D,E是半圆上的点且CD与BE交于点F,用①![]() ,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
A.0B.1C.2D.3
【答案】D
【解析】
连接OE、OD,
(1)当![]() ,DC⊥AB时,由圆周角定理可得∠EOD=∠DOB,根据等腰三角形的性质可得OF⊥BE,由CD⊥AB可得∠OFB=∠OCD=90°,利用AAS可证明△OCD≌OFB,可得∠ODC=∠OBF,根据等腰三角形的性质可得∠OBD=∠ODB,利用角的和差关系可得∠FBD=∠FDB,即可证明FB=FD;
,DC⊥AB时,由圆周角定理可得∠EOD=∠DOB,根据等腰三角形的性质可得OF⊥BE,由CD⊥AB可得∠OFB=∠OCD=90°,利用AAS可证明△OCD≌OFB,可得∠ODC=∠OBF,根据等腰三角形的性质可得∠OBD=∠ODB,利用角的和差关系可得∠FBD=∠FDB,即可证明FB=FD;
(2)当![]() ,FB=FD时,同(1)可得OF⊥BE,根据等腰三角形的性质可得∠OBD=∠ODB,∠FBD=∠FDB,利用角的和差关系可得∠ODC=∠OBF,利用ASA可证明△OCD≌OFB,可得∠OFB=∠OCD=90°,可得DC⊥AB;
,FB=FD时,同(1)可得OF⊥BE,根据等腰三角形的性质可得∠OBD=∠ODB,∠FBD=∠FDB,利用角的和差关系可得∠ODC=∠OBF,利用ASA可证明△OCD≌OFB,可得∠OFB=∠OCD=90°,可得DC⊥AB;
(3)当DC⊥AB,FB=FD时,同(2)可得△OCD≌OFB,由DC⊥AB可得∠OFB=∠OCD=90°,根据垂径定理可得![]() ,综上即可得答案.
,综上即可得答案.
如图,连接OE、OD,
(1)当![]() ,DC⊥AB时,
,DC⊥AB时,
∵![]() ,OD为半径,
,OD为半径,
∴∠EOD=∠DOB,
∵OE=OB,
∴OF⊥BE,
∴∠OFB=90°,
∵DC⊥AB,
∴∠DCB=∠OFB=90°,
在△OCD和△OFB中, ,
,
∴△OCD≌△OFB,
∴∠ODC=∠OBF,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠OBD-∠OBF=∠ODB-∠ODC,即∠FDB=∠FBD,
∴FB=FD.
(2)当![]() ,FB=FD时,
,FB=FD时,
∵![]() ,OD为半径,
,OD为半径,
∴∠EOD=∠DOB,
∵OE=OB,
∴OF⊥BE,
∴∠OFB=90°,
∵OD=OB,FB=FD,
∴∠ODB=∠OBD,∠FDB=∠FBD,
∴∠ODC=∠OBF,
在△OCD和△OFB中, ,
,
∴△OCD≌△OFB,
∴∠OCD=∠OFB=90°,
∴DC⊥AB.
(3)当DC⊥AB,FB=FD时,
∵DC⊥AB,
∴∠OCD=90°,
∵OD=OB,FB=FD,
∴∠ODB=∠OBD,∠FDB=∠FBD,
∴∠ODC=∠OBF,
在△OCD和△OFB中, ,
,
∴△OCD≌△OFB,
∴∠OFB=∠OCD=90°,
∴OD⊥BE,
∵OD是半径,
∴![]() .
.

综上所述,组成真命题的个数为3,
故选:D.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
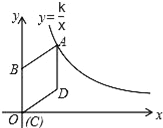
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=![]() (x>0)的图象上,点D的坐标为(4,3).
(x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)将这个菱形沿x轴正方向平移,当顶点D落在反比例函数图象上时,求菱形平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查(每个被调查的对象必须选择而且只能在四种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整).

(1)这次调查中,一共调查了________名学生;
(2)请补全两幅统计图;
(3)若有3名喜欢跳绳的学生,1名喜欢足球的学生组队外出参加一次联谊活动,欲从中选出2人担任组长(不分正副),求一人是喜欢跳绳、一人是喜欢足球的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数![]() 的图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为P.
的图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为P.
(1)直接写出点A,C,P的坐标.
(2)画出这个函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
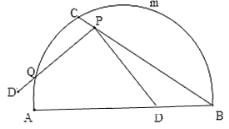
【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
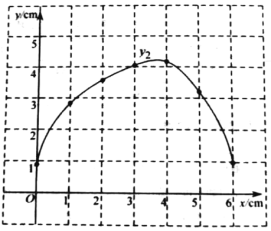
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小石设计的“过圆上一点作圆的切线”的尺规作图的过程.
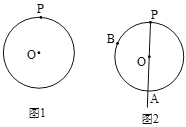
已知:如图1,![]() 及
及![]() 上一点P.
上一点P.
求作:直线PQ,使得PQ与![]() 相切.
相切.
作法:如图2,
①连接PO并延长交![]() 于点A;
于点A;
②在![]() 上任取一点B(点P,A除外),以点B为圆心,BP长为半径作
上任取一点B(点P,A除外),以点B为圆心,BP长为半径作![]() ,与射线PO的另一个交点为C.
,与射线PO的另一个交点为C.
③连接CB并延长交![]() 于点Q.
于点Q.
④作直线PQ;
所以直线PQ就是所求作的直线.
根据小石设计的尺规作图的过程.
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下面的证明.
证明:∵CQ是的![]() 直径,
直径,
∴![]() ________
________![]() (________________)(填推理的依据)
(________________)(填推理的依据)
∴![]() .
.
又∵OP是![]() 的半径,
的半径,
∴PQ是![]() 的切线(________________)(填推理的依据)
的切线(________________)(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE,连接DE并延长交射线AP于点F,连接BF

(1)若![]() ,直接写出
,直接写出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求证:![]() .
.
(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一段长为28m的铁丝网与一面长为8m的墙面围成一个矩形菜园,为了使菜园面积尽可能的大,给出了甲、乙两种围法,请通过计算来说明这个菜园长、宽各为多少时,面积最大?最大面积是多少?
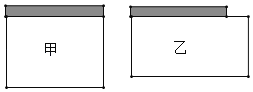
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com