
如图1,直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0)。

(1)m为何值时,△OAB面积最大?最大值是多少?
(2)如图2,在(1)的条件下,函数 的图像与直线AB相交于C、D两点,若
的图像与直线AB相交于C、D两点,若 ,求k的值。
,求k的值。
(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10)。
(1)当m =10时,△OAB面积最大,最大值是50(2)9(3)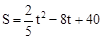 (0<t<10)
(0<t<10)
【解析】解:(1)∵直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0),
∴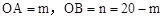 。
。
∴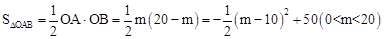 。
。
∴当m =10时,△OAB面积最大,最大值是50。
(2)当m =10时,直线AB解析式为。
由对称性,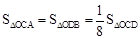 ,
,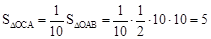 。
。
∴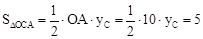 。∴
。∴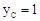 。
。
∵点C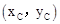 在直线AB上,∴
在直线AB上,∴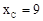 。
。
∴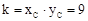 。
。
(3)如图,C(9,1),D(1,9)移动后的重叠部分为△O′C′D′,时间t时,点O′的坐标为(t,0)。
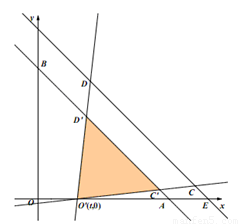
由(2)知,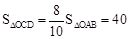 。
。
∵C′D′∥CD,∴△O′C′D′∽△OCD,△O′C′A∽△OCE。
∴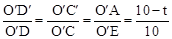 ,
,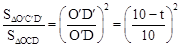 。
。
∴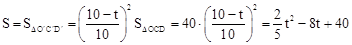 。
。
∴S与运动时间t(秒)的函数关系式为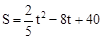 (0<t<10)。
(0<t<10)。
(1)求出△OAB面积关于m的函数关系式,应用二次函数最值求解。
(2)由反比例函数和直线的对称性,根据曲线上点的坐标与方程的关系求解。
(3)应用△O′C′D′∽△OCD,△O′C′A∽△OCE建立比例式求解。


科目:初中数学 来源: 题型:
| k |
| x |
| 1 |
| 8 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 的图象与直线AB相交于C、D两点,若
的图象与直线AB相交于C、D两点,若 ,求k的值.
,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0)。

(1)m为何值时,△OAB面积最大?最大值是多少?
(2)如图2,在(1)的条件下,函数![]() 的图像与直线AB相交于C、D两点,若
的图像与直线AB相交于C、D两点,若![]() ,求k的值。
,求k的值。
(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10)。
查看答案和解析>>
科目:初中数学 来源:2013年广东省深圳市中考数学试卷(解析版) 题型:解答题
 的图象与直线AB相交于C、D两点,若
的图象与直线AB相交于C、D两点,若 ,求k的值.
,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com