
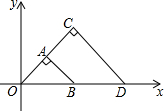
 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:4,∠OCD=90°,CO=CD.若点B的坐标为(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:4,∠OCD=90°,CO=CD.若点B的坐标为(1,0),则点C的坐标为( )| A. | (2,2) | B. | (2,4) | C. | (2$\sqrt{2},2\sqrt{2}$) | D. | (4,2) |
分析 首先利用等腰直角三角形的性质得出A点坐标,再利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,ky),进而求出即可.
解答 解:∵∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,点B的坐标为(1,0),
∴BO=1,则AO=AB=$\frac{\sqrt{2}}{2}$,
∴A($\frac{1}{2}$,$\frac{1}{2}$),
∵等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:4,
∴点C的坐标为:(2,2).
故选:A.
点评 此题主要考查了位似变换的性质,正确理解位似与相似的关系,记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键.


科目:初中数学 来源: 题型:解答题
 已知,如图,A(-4,2),B(n,-4)是一次函数y1=k1+b图象与反比例函数y2=$\frac{{k}_{1}}{x}$的图象的两个交点.
已知,如图,A(-4,2),B(n,-4)是一次函数y1=k1+b图象与反比例函数y2=$\frac{{k}_{1}}{x}$的图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
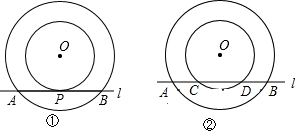 我们知道,求圆环的面积可以转化为求大圆与小圆面积的差.
我们知道,求圆环的面积可以转化为求大圆与小圆面积的差.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,它正在播新闻 | |
| B. | 度量三角形的内角和,结果是180° | |
| C. | 一个袋中装有6个黑球,从中摸出一个白球 | |
| D. | 抛掷5枚硬币,结果是3个正面朝上与3个反面朝上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△OBA∽△DOC,边OA、OC都在x轴的正半轴上,点B的坐标为(5,12),∠BAO=∠OCD=90°,点D在第一象限,OD=6.5,函数y=$\frac{k}{x}$(x>0)的图象经过点D,交AB边于点E.
如图,在平面直角坐标系中,△OBA∽△DOC,边OA、OC都在x轴的正半轴上,点B的坐标为(5,12),∠BAO=∠OCD=90°,点D在第一象限,OD=6.5,函数y=$\frac{k}{x}$(x>0)的图象经过点D,交AB边于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com