
 某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )| A. | 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球 | |
| B. | 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6 | |
| C. | 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” | |
| D. | 掷一枚质地均匀的硬币,落地时结果是“正面向上” |
分析 分别计算出每个事件的概率,其值约为0.16的即符合题意;
解答 解:A、袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球的概率为$\frac{2}{3}$,不符合题意;
B、掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6的概率为$\frac{1}{6}$,符合题意;
C、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率为$\frac{1}{3}$,不符合题意;
D、掷一枚质地均匀的硬币,落地时结果是“正面向上”的概率为$\frac{1}{2}$,不符合题意;
故选:B.
点评 本题主要考查概率的计算和频率估计概率思想,注意这种概率的得出是在大量实验的基础上得出的,不能单纯的依靠几次决定.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{6}^{2}+{8}^{2}}$=6+8=14 | B. | $\sqrt{(-16)×(-25)}$=$\sqrt{-16}$•$\sqrt{-25}$=(-4)×(-5)=20 | ||
| C. | $\sqrt{4\frac{9}{25}}$=$\sqrt{4}$•$\sqrt{\frac{9}{25}}$=2×$\frac{3}{5}$=$\frac{6}{5}$ | D. | $\frac{\sqrt{24}}{\sqrt{3}}$=$\sqrt{\frac{24}{3}}$=$\sqrt{8}$=2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
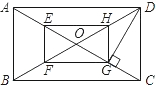 如图,O是矩形ABCD的对角线的交点,E,F,G,H分别是OA,OB,OC,OD的中点;
如图,O是矩形ABCD的对角线的交点,E,F,G,H分别是OA,OB,OC,OD的中点;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,AB⊥BC于点B,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,同时点Q从点C出发,以3cm/s的速度向点B运动,其中一个动点到达端点时另一个动点也随之停止运动,设运动时间为ts.
如图,在四边形ABCD中,AD∥BC,AB⊥BC于点B,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动,同时点Q从点C出发,以3cm/s的速度向点B运动,其中一个动点到达端点时另一个动点也随之停止运动,设运动时间为ts.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com