
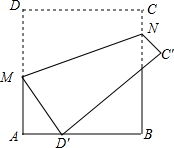
 如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为2$\sqrt{10}$.
如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为2$\sqrt{10}$. 分析 作NF⊥AD,垂足为F,连接DD′,ND′,根据图形折叠的性质得出DD′⊥MN,先证明△DAD′∽△DEM,再证明△NFM≌△DAD′,然后利用勾股定理的知识求出MN的长.
解答 解:作NF⊥AD,垂足为F,连接DD′,ND′,
∵将正方形纸片ABCD折叠,使得点D落在边AB上的D′点,折痕为MN,
∴DD′⊥MN,
∵∠A=∠DEM=90°,∠ADD′=∠EDM,
∴△DAD′∽△DEM,
∴∠DD′A=∠DME,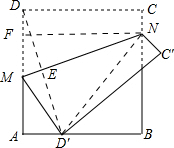
在△NFM和△DAD′中
$\left\{\begin{array}{l}{∠DD′A=∠NMF}\\{∠A=∠NFM}\\{NF=DA}\end{array}\right.$,
∴△NFM≌△DAD′(AAS),
∴FM=AD′=2cm,
又∵在Rt△MNF中,FN=6cm,
∴根据勾股定理得:MN=$\sqrt{F{N}^{2}+F{M}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$.
故答案为:2$\sqrt{10}$.
点评 此题主要考查了图形的翻折变换,根据图形折叠前后图形不发生大小变化得出三角形的全等是解决问题的关键,难度一般.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
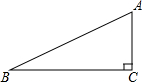 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )| A. | 5÷tan26°= | B. | 5÷sin26°= | C. | 5×cos26°= | D. | 5×tan26°= |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
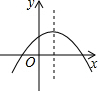 二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象可能是( )
二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象可能是( )| A. | 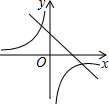 | B. |  | C. | 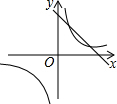 | D. | 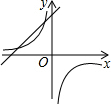 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
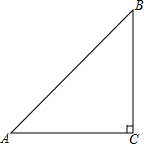 如图,已知Rt△ACB中,∠C=90°,∠BAC=45°.
如图,已知Rt△ACB中,∠C=90°,∠BAC=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
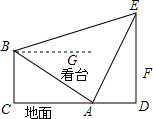 如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10$\sqrt{3}$,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10$\sqrt{3}$,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
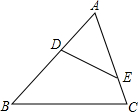 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )| A. | ∠AED=∠B | B. | ∠ADE=∠C | C. | $\frac{AD}{AE}$=$\frac{AC}{AB}$ | D. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com