
如图,在∠AOD的内部作射线OB,使∠AOB=∠COD,则图中还有哪些相等的角____________________.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
| m | x |
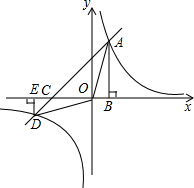 内的交点,且S△AOB=3.
内的交点,且S△AOB=3.查看答案和解析>>
科目:初中数学 来源: 题型:
 D分别交AB,CD于点E,F.
D分别交AB,CD于点E,F.| OA |
| OC |
| OD |
| OB |
| OE |
| AD |
| OF |
| BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•清流县质检)星期天,小明在解答下列题目时卡壳了.
(2011•清流县质检)星期天,小明在解答下列题目时卡壳了.| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=| m |
| x |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 请将下面证明中每一步的理由填在括号内:
请将下面证明中每一步的理由填在括号内:| 1 |
| 2 |
| 1 |
| 2 |
| 180°-120° |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com