
【题目】(方法提炼)
解答几何问题常常需要添辅助线,其中平移图形是重要的添辅助线策略.
(问题情境)
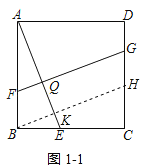
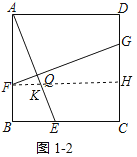
如图1,在正方形ABCD中,E,F,G分别是BC,AB,CD上的点,FG⊥AE于点Q.求证:AE=FG.
小明在分析解题思路时想到了两种平移法:
方法1:平移线段FG使点F与点B重合,构造全等三角形;
方法2:平移线段BC使点B与点F重合,构造全等三角形;
(尝试应用)
(1)请按照小明的思路,选择其中一种方法进行证明;
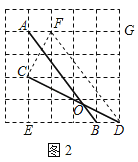
(2)如图2,正方形网格中,点A,B,C,D为格点,AB交CD于点O.求tan∠AOC的值;
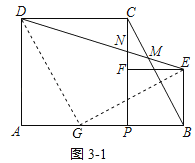
(3)如图3,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连结DE分别交线段BC,PC于点M,N.
①求∠DMC的度数;
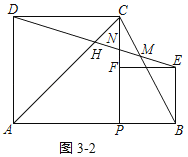
②连结AC交DE于点H,求![]() 的值.
的值.

【答案】(1)证明见解析;(2)![]() ;(3)①∠DMC=45°;②
;(3)①∠DMC=45°;②![]() .
.
【解析】
(1)①平移线段FG至BH交AE于点K,证明四边形BFGH是平行四边形,得出BH=FG,由ASA证得△ABE≌△CBH,即可得出结论;
②平移线段BC至FH交AE于点K,则四边形BCHF是矩形,由ASA证得△ABE≌△FHG,即可得出结论;
(2)将线段AB向右平移至FD处,使得点B与点D重合,连接CF,设正方形网格的边长为单位1,由勾股定理求得CF=![]() ,CD=2
,CD=2![]() ,DF=5,得出CF2+CD2=DF2,则∠FCD=90°,由tan∠AOC=tan∠FDC=
,DF=5,得出CF2+CD2=DF2,则∠FCD=90°,由tan∠AOC=tan∠FDC=![]() 即可得出结果;
即可得出结果;
(3)①平移线段BC至DG处,连接GE,由SAS证得△AGD≌△BEG,得出DG=EG,∠ADG=∠EGB,证明∠EGD=90°,得出∠GDE=∠GED=45°,即可得出结果;
②证明△ADH∽△ACB,得出![]() =
=![]() =
=![]() .
.
(1)①平移线段FG至BH交AE于点K,如图1﹣1所示:
由平移的性质得:FG//BH,
∵四边形ABCD是正方形,
∴AB//CD,AB=BC,∠ABE=∠C=90°,
∴四边形BFGH是平行四边形,
∴BH=FG,
∵FG⊥AE,
∴BH⊥AE,
∴∠BKE=90°,
∴∠KBE+∠BEK=90°,
∵∠BEK+∠BAE=90°,
∴∠BAE=∠CBH,
在△ABE和△CBH中,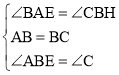 ,
,
∴△ABE≌△CBH(ASA),
∴AE=BH,
∴AE=FG;
②平移线段BC至FH交AE于点K,如图1﹣2所示:
则四边形BCHF是矩形,∠AKF=∠AEB,
∴FH=BC,∠FHG=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠ABE=90°,
∴AB=FH,∠ABE=∠FHG,
∵FG⊥AE,
∴∠HFG+∠AKF=90°,
∵∠AEB+∠BAE=90°,
∴∠BAE=∠HFG,
在△ABE和△FHG中,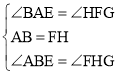 ,
,
∴△ABE≌△FHG(ASA),
∴AE=FG;
(2)将线段AB向右平移至FD处,使得点B与点D重合,连接CF,如图2所示:
∴∠AOC=∠FDC,
设正方形网格的边长为单位1,
则AC=2,AF=1,CE=2,DE=4,FG=3,DG=4,
根据勾股定理可得:CF=![]() =
=![]() =
=![]() ,CD=
,CD=![]() =
=![]() =2
=2![]() ,DF=
,DF=![]() =
=![]() =5,
=5,
∵(![]() )2+(2
)2+(2![]() )2=52,
)2=52,
∴CF2+CD2=DF2,
∴∠FCD=90°,
∴tan∠AOC=tan∠FDC=![]() =
=![]() =
=![]() ;
;
(3)①平移线段BC至DG处,连接GE,如图3﹣1所示:
则∠DMC=∠GDE,四边形DGBC是平行四边形,
∴DC=GB,
∵四边形ADCP与四边形PBEF都是正方形,
∴DC=AD=AP,BP=BE,∠DAG=∠GBE=90°
∴DC=AD=AP=GB,
∴AG=BP=BE,
在△AGD和△BEG中,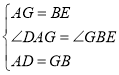 ,
,
∴△AGD≌△BEG(SAS),
∴DG=EG,∠ADG=∠EGB,
∴∠EGB+∠AGD=∠ADG+∠AGD=90°,
∴∠EGD=90°,
∴∠GDE=∠GED=45°,
∴∠DMC=∠GDE=45°;
②如图3﹣2所示:
∵AC为正方形ADCP的对角线,
∴∠DAC=∠PAC=∠DMC=45°,
∴AC=![]() AD,
AD,
∵∠HCM=∠BCA,
∴∠AHD=∠CHM=∠ABC,
∴△ADH∽△ACB,
∴![]() =
=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】小腾的爸爸计划将一笔资金用于不超过10天的短期投资,针对这笔资金,银行专属客户经理提供了三种投资方案,这三种方案的回报如下:
方案一:每一天回报30元;
方案二:第一天回报8元,以后每一天比前一天多回报8元;
方案三:第一天回报0.5元,以后每一天的回报是前一天的2倍.
下面是小腾帮助爸爸选择方案的探究过程,请补充完整:
(1)确定不同天数所得回报金额(不足一天按一天计算),如下表:
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
方案一 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
方案二 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
方案三 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
|
其中![]() ________;
________;
(2)计算累计回报金额,设投资天数为![]() (单位:天),所得累计回报金额是
(单位:天),所得累计回报金额是![]() (单位:元),于是得到三种方案的累计回报金额
(单位:元),于是得到三种方案的累计回报金额![]() ,
,![]() ,
,![]() 与投资天数
与投资天数![]() 的几组对应值:
的几组对应值:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
| 8 | 24 | 48 | 80 | 120 | 168 | 224 | 288 | 360 | 440 |
| 0.5 | 1.5 | 3.5 | 7.5 | 15.5 | 31.5 | 63.5 | 127.5 | 255.5 |
|
其中![]() ________;
________;
(3)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,
,![]() ,并画出
,并画出![]() ,
,![]() ,
,![]() 的图象;
的图象;
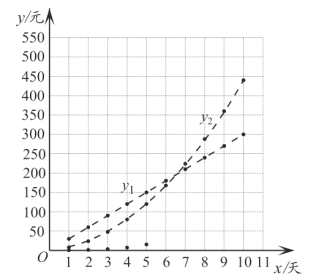
注:为了便于分析,用虚线连接离散的点.
(4)结合图象,小腾给出了依据不同的天数而选择对应方案的建议:
_________________________________________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“过直线外一点作已知直线的平行线“的尺规作图过程.

已知:如图,直线![]() 和直线
和直线![]() 外一点
外一点![]() .
.
求作:直线![]() ,使直线
,使直线![]() 直线
直线![]() .
.
作法:如图,
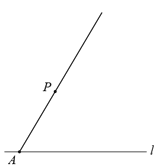
①在直线![]() 上任取一点
上任取一点![]() ,作射线
,作射线![]() ;
;
②以![]() 为圆心,
为圆心,![]() 为半径作弧,交直线
为半径作弧,交直线![]() 于点
于点![]() ,连接
,连接![]() ;
;
③以![]() 为圆心,
为圆心,![]() 长为半径作弧,交射线
长为半径作弧,交射线![]() 于点
于点![]() ;分别以
;分别以![]() 为圆心,大于
为圆心,大于![]() 长为半径作弧,在
长为半径作弧,在![]() 的右侧两弧交于点
的右侧两弧交于点![]() ;
;
④作直线![]() ;
;
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图中的图形;
(2)完成下面的证明:
证明:由作图可知![]() 平分
平分![]() ,
,
![]() .
.
又![]() ,
,
![]() .(_______________________________)(填依据1).
.(_______________________________)(填依据1).
![]() ,
,
![]() .
.
![]() ,∴直线
,∴直线![]() 直线
直线![]() .(______________________)(填依据2).
.(______________________)(填依据2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了解初中学生参加综合实践活动的情况,随机抽取了本市初一、初二、初三年级各![]() 名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.
名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.

(1)在被调查的学生中,参加综合实践活动的有多少人,参加科技活动的有多少人;
(2)如果本市有![]() 万名初中学生,请你估计参加科技活动的学生约有多少名.
万名初中学生,请你估计参加科技活动的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生的安全意识,在全校范围内随机抽取部分学生进行问卷调查.根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制如下两幅尚不完整的统计图.
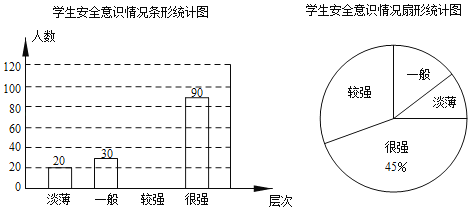
根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生,将条形统计图补充完整;
(2)扇形统计图中,“较强”层次所占圆心角的大小为 °;
(3)若该校有1900名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,请你估计全校需要强化安全教育的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
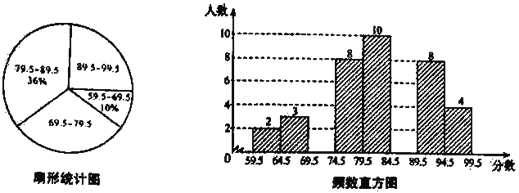
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
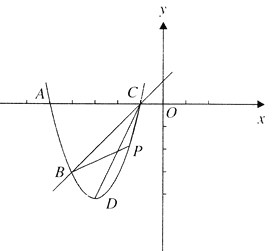
【题目】如图,已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,
两点,![]() 为顶点,
为顶点,![]() 为抛物线上一动点(与点
为抛物线上一动点(与点![]() 不重合)
不重合)
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 当点
当点![]() 在直线
在直线![]() 的下方运动时,求
的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
![]() 该抛物线上是否存在点
该抛物线上是否存在点![]() ,使
,使![]() ?若存在,求出所有点
?若存在,求出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场计划今年养殖无公害标准化龙虾和鲤鱼,由于受养殖水面的制约,这两个品种的苗种的总投放量只有50吨.根据经验测算,这两个品种的种苗每投放一吨的先期投资、养殖期间的投资以及产值如下表:(单位:千元/吨)
品种 | 先期投资 | 养殖期间投资 | 产值 |
鲤鱼 | 9 | 3 | 30 |
龙虾 | 4 | 10 | 20 |
养殖场受经济条件的影响,先期投资不超过360千元,养殖期间的投资不超过290千元.设鲤鱼种苗的投放量为x吨.
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(千元),试写出y与x之间的函数关系式,并求出当x等于多少时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形![]() 中,对角线
中,对角线![]() 平分
平分![]() .为了研究图中线段之间的数量关系,设
.为了研究图中线段之间的数量关系,设![]() .
.
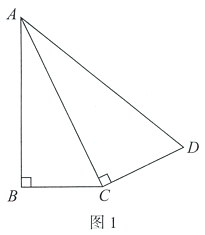
(1)由题意可得![]() ,(在括号内填入图1中相应的线段)y关于x的函数表达式为
,(在括号内填入图1中相应的线段)y关于x的函数表达式为![]() ________;
________;
(2)如图2,在平面直角坐标系![]() 中,根据(1)中y关于x的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;
中,根据(1)中y关于x的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;
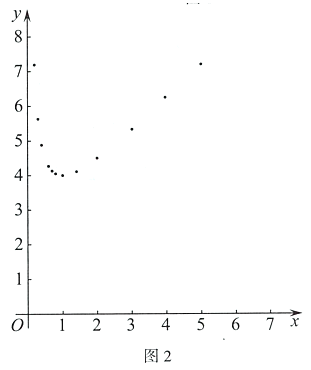
(3)结合函数图象,解决问题:
①写出该函数的一条性质:__________________________;
②估计![]() 的最小值为__________.(结果精确到0.1)
的最小值为__________.(结果精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com