
分析 在AC上截取AE'=AE,①当E'和F重合时,可先证明△AOE≌△AOF,△BOE≌△COF,从而得到AB=AE+BE=AF+CF=AC,故△ABC是等腰三角形;②如果E'和F不重合,易知△AOE'≌△AOF,于是OE'=OF,即∠OFE'=∠BEC,从而得到$∠A+\frac{1}{2}∠C=\frac{1}{2}∠B+∠C$,结合三角形的内角和定理可求得∠A=60°.
解答 证明:在AC上截取AE'=AE.
①当点E'和F重合时,如图1所示:连接OA
在△AEO和△AFO中,$\left\{\begin{array}{l}{AE=AF}\\{EO=OF}\\{AO=AO}\end{array}\right.$,
∴△AEO≌△AFO.
∴∠AEO=∠AFO.
∴∠BEO=∠CFO.
在△BEO和△CFO中,$\left\{\begin{array}{l}{∠BEO=∠CFO}\\{OE=OF}\\{∠EOB=∠FOC}\end{array}\right.$,
∴△BEO≌△CFO.
∴BE=FC.
∴AE+BE=AF+CF.
∴AB=AC.
∴△ABC是等腰三角形.
②当点E′与点F不重合时,如图2所示:连接OA.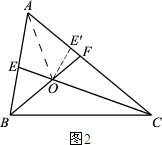
∵O是△ABC的内心,
∴∠EAO=∠E′AO.
在△AEO和△AE′O中,$\left\{\begin{array}{l}{AE=AE′}\\{∠EAO=∠E′AO}\\{AO=AO}\end{array}\right.$,
∴△AEO≌△AE′O.
∴OE=OE′,∠AEO=∠AE′O.
∴∠BEC=∠OE′C.
∵OE=OF,
∴OE′=OF.
∴∠OE′F=∠OFE′.
∴∠BEC=∠OFE',即$∠A+\frac{1}{2}∠C$=$\frac{1}{2}∠B+∠C$.
∴∠A=$\frac{1}{2}∠B+\frac{1}{2}∠C$=$\frac{1}{2}$(∠B+∠C),即$∠A=\frac{1}{2}×(180°-∠A)$.
解得:∠A=60°.
综上所述,△ABC是等腰三角形或∠A=60°.
点评 本题主要考查的是三角形的内心、全等三角形的性质和判定、三角形内角和定理的应用,分类讨论是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,三角形ABC的三条边长都是2厘米,分别以线段AB、BC、CA的中点D、E、F为圆心,2厘米为直径画半圆.
如图,三角形ABC的三条边长都是2厘米,分别以线段AB、BC、CA的中点D、E、F为圆心,2厘米为直径画半圆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 1 | 2 | 3 | 4 | 5 |
| 用水量(吨) | 8 | 10 | 11 | 15 | 18 |
| 费用(元) | 16 | 20 | 23 | 35 | 44 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将△ABC沿AB边平移得到△A1B1C1,若它们的重叠部分的面积为△ABC面积的$\frac{4}{25}$,AB=4,则三角形移动的距离AA1=2.4.
如图,将△ABC沿AB边平移得到△A1B1C1,若它们的重叠部分的面积为△ABC面积的$\frac{4}{25}$,AB=4,则三角形移动的距离AA1=2.4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 给出两个等边三角形纸片如图,要求用一个剪成底面是等边三角形的三棱锥,另一个剪成底面是等边三角形的直三棱柱,请你设计一种剪拼的方法,分别在图上用虚线画出来.
给出两个等边三角形纸片如图,要求用一个剪成底面是等边三角形的三棱锥,另一个剪成底面是等边三角形的直三棱柱,请你设计一种剪拼的方法,分别在图上用虚线画出来.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com