
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
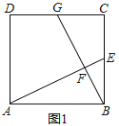
аЁУїгіЕНетбљвЛИіЮЪЬтЃКШчЭМ1ЃЌдке§ЗНаЮABCDжаЃЌЕуEЪЧБпBCЕФжаЕуЃЌЕуFЪЧЯпЖЮAEЩЯвЛЕуЃЌBFЕФбгГЄЯпНЛЩфЯпCDгкЕуGЃЌШєAB=6ЃЌAF=4EFЃЌЧѓCGЕФжЕгыЁЯAFBЕФЖШЪ§ЃЎ
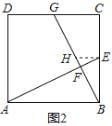
ЫћЕФзіЗЈЪЧЃКЙ§ЕуEзїEHЁЮABНЛBGгкЕуHЃЌЕУЕНЁїBAFЁзЁїHEFЃЈШчЭМ2ЃЉЃЎ
ЃЈ1ЃЉCGЕШгкЖрЩйЃЌЁЯAFBЕШгкЖрЩйЖШЃЛ
ВЮПМаЁУїЫМПМЮЪЬтЕФЗНЗЈЃЌНтОіЯТСаЮЪЬтЃЛ
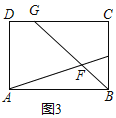
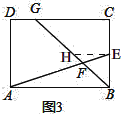
ЃЈ2ЃЉШчЭМ3ЃЌдкОиаЮABCDжаЃЌЕуEЪЧБпBCЕФжаЕуЃЌЕуFЪЧЯпЖЮAEЩЯвЛЕуЃЌBFЕФбгГЄЯпНЛЩфЯпCDгкЕуGЃЌШєAF=3EFЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
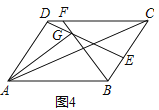
ЃЈ3ЃЉШчЭМ4ЃЌдкЦНааЫФБпаЮABCDжаЃЌEЁЂFЗжБ№ЪЧБпBCЁЂCDЩЯЕФЕуЃЌBFКЭDEЯрНЛгкЕуGЃЌЧвAB=kADЃЌЁЯDAG=ЁЯBACЃЌЧѓГі![]() ЕФжЕЃЈгУКЌkЕФЪНзгБэЪОЃЉ
ЕФжЕЃЈгУКЌkЕФЪНзгБэЪОЃЉ
ЁОД№АИЁПЃЈ1ЃЉCG=3ЃЌЁЯAFB=90ЁуЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуEзїEHЁЮCDНЛBGгкЕуHЃЌИљОне§ЗНаЮЕФаджЪКЭЯрЫЦШ§НЧаЮЕФХаЖЈЖЈРэЕУЕНЁїEFHЁзЁїAFBЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУЕНCG=![]() AB=3ЃЛ
AB=3ЃЛ
ЃЈ2ЃЉЗТееЃЈ1ЃЉЕФНтД№ЫМТЗМЦЫуМДПЩЃЛ
ЃЈ3ЃЉбгГЄAGНЛDCгкMЃЌбгГЄDEНЛABЕФбгГЄЯпгкNЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЖЈРэКЭаджЪЖЈРэНтД№ЃЎ
ЃЈ1ЃЉЙ§ЕуEзїEHЁЮCDНЛBGгкЕуHЃЌ
ЁрЁїBEHЁзЁїBCGЃЌЁр![]() ЃЌ
ЃЌ
ЁпЕуEЪЧБпBCЕФжаЕуЃЌЁрBC=2BEЃЌЁрCG=2HEЃЌ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌЁрABЁЮCDЃЌ
ЁрEHЁЮABЃЌЁрЁїEFHЁзЁїAFBЃЌ
Ёр![]() ЃЌЁпAF=4EFЃЌЁрAB=4EHЃЌ
ЃЌЁпAF=4EFЃЌЁрAB=4EHЃЌ
ЁрCG=![]() AB=3ЃЌЁпCD=6ЃЌЁрCG=BEЃЌ
AB=3ЃЌЁпCD=6ЃЌЁрCG=BEЃЌ
дкЁїABEКЭЁїBCGжаЃЌ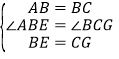 ЃЌ
ЃЌ
ЁрЁїABEЁеЁїBCGЃЌЁрЁЯBAE=ЁЯCBGЃЌ
ЁпЁЯABF+ЁЯCBG=90ЁуЃЌЁрЁЯBAE+ЁЯABF=90ЁуЃЌЁрЁЯAFB=90ЁуЃЌ
ЃЈ2ЃЉШчЭМ3ЃЌЭЌЃЈ1ЃЉЗНЗЈЕУГіЃЌCG=2HEЃЌ
ЭЌЃЈ1ЃЉЕФЗНЗЈЕУГіЃЌ![]() ЃЌ
ЃЌ
ЁпAF=3EFЃЌЁрAB=3EHЃЌЁрEH=![]() ABЃЌ
ABЃЌ
ЁрCG=2EH=![]() ABЃЌЁр
ABЃЌЁр![]() ЃЛ
ЃЛ
ЃЈ3ЃЉбгГЄAGНЛDCгкMЃЌбгГЄDEНЛABЕФбгГЄЯпгкNЃЌ
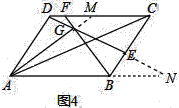
ЁпЁЯDAG=ЁЯBACЃЌЁЯADM=ЁЯABCЃЌ
ЁрЁїADMЁзЁїABCЃЌЁр![]() =kЃЌ
=kЃЌ
ЁпЕуEЪЧБпBCЕФжаЕуЃЌЁр![]() ЃЌ
ЃЌ
ЁпDCЁЮABЃЌЕуEЪЧБпBCЕФжаЕуЃЌ
ЁрAB=DC=BNЃЌЁпDCЁЮABЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌгжAB=
ЃЌгжAB=![]() ANЃЌ
ANЃЌ
ЁрDF=![]() DMЃЌгж
DMЃЌгж![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФЖЅЕуAЁЂCЕФзјБъЗжБ№ЮЊЃЈ10ЃЌ0ЃЉЃЌЃЈ0ЃЌ4ЃЉЃЌЕуDЪЧOAЕФжаЕуЃЌЕуPдкBCЩЯдЫЖЏЃЌЕБЁїODPЪЧбќГЄЮЊ5ЕФЕШбќШ§НЧаЮЪБЃЌЕуPЕФзјБъЮЊ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
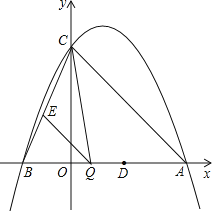
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЖўДЮКЏЪ§y=ax2-2ax+cЃЈaЁй0ЃЉЕФЭМЯѓгыyжсНЛгкЕуCЃЈ0ЃЌ4ЃЉЃЌгыxжсНЛгкЕуAЁЂBЃЌЕуAЕФзјБъЮЊЃЈ4ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉаДГіИУЖўДЮКЏЪ§ЕФЖдГЦжсКЭЖЅЕузјБъЃЛ
ЃЈ3ЃЉЕуQЪЧЯпЖЮABЩЯЕФЖЏЕуЃЌЙ§ЕуQзїQEЁЮACЃЌНЛBCгкЕуEЃЌСЌНгCQЃЎЕБЁїCQEЕФУцЛ§зюДѓЪБЃЌЧѓЕуQЕФзјБъЃЛ
ЃЈ4ЃЉШєЦНаагкxжсЕФЖЏжБЯпlгыИУХзЮяЯпНЛгкЕуPЃЌгыжБЯпACНЛгкЕуFЃЌЕуDЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЎЮЪЃКЪЧЗёДцдкетбљЕФжБЯпlЃЌЪЙЕУЁїODFЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНx2Љ2xЉ3ЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌдђЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
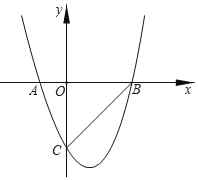
A. ABЃН4
B. ЁЯABCЃН45Ёу
C. ЕБxЃО0ЪБЃЌyЃМЉ3
D. ЕБxЃО1ЪБЃЌyЫцxЕФдіДѓЖјдіДѓ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
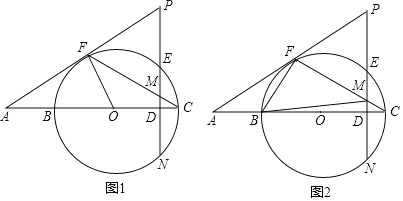
ЁОЬтФПЁПШчЭМ1ЃЌDЪЧЁбOЕФжБОЖBCЩЯЕФвЛЕуЃЌЙ§DзїDEЁЭBCНЛЁбOгкEЁЂNЃЌFЪЧЁбOЩЯЕФвЛЕуЃЌЙ§FЕФжБЯпЗжБ№гыCBЁЂDEЕФбгГЄЯпЯрНЛгкAЁЂPЃЌСЌНсCFНЛPDгкMЃЌЁЯCЃН![]() ЁЯPЃЎ
ЁЯPЃЎ
ЃЈ1ЃЉЧѓжЄЃКPAЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁЯAЃН30ЁуЃЌЁбOЕФАыОЖЮЊ4ЃЌDMЃН1ЃЌЧѓPMЕФГЄЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНсBFЁЂBMЃЛдкЯпЖЮDNЩЯгавЛЕуHЃЌВЂЧввдHЁЂDЁЂCЮЊЖЅЕуЕФШ§НЧаЮгыЁїBFMЯрЫЦЃЌЧѓDHЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§![]() ЗжБ№НЛyжсЁЂxжсгкAЁЂBСНЕуЃЌХзЮяЯпy=Љx2+bx+cЙ§AЁЂBСНЕуЃЎ
ЗжБ№НЛyжсЁЂxжсгкAЁЂBСНЕуЃЌХзЮяЯпy=Љx2+bx+cЙ§AЁЂBСНЕуЃЎ
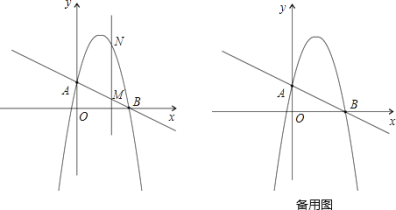
ЃЈ1ЃЉЧѓетИіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉзїДЙжБxжсЕФжБЯпx=tЃЌдкЕквЛЯѓЯоНЛжБЯпABгкMЃЌНЛетИіХзЮяЯпгкNЃЎЧѓЕБtШЁКЮжЕЪБЃЌMNгазюДѓжЕЃПзюДѓжЕЪЧЖрЩйЃП
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЧщПіЯТЃЌвдAЁЂMЁЂNЁЂDЮЊЖЅЕузїЦНааЫФБпаЮЃЌЧѓЕкЫФИіЖЅЕуDЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
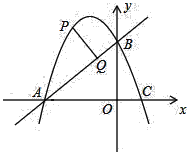
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§yЃНЉx2+bx+3ЕФЭМЯѓгыxжсНЛгкAЁЂCСНЕуЃЈЕуAдкЕуCЕФзѓВрЃЉЃЌгыyжсНЛгкЕуBЃЌЧвOAЃНOBЃЎ
ЃЈ1ЃЉЧѓЯпЖЮACЕФГЄЖШЃЛ
ЃЈ2ЃЉШєЕуPдкХзЮяЯпЩЯЃЌЕуPЮЛгкЕкЖўЯѓЯоЃЌЙ§PзїPQЁЭABЃЌДЙзуЮЊQЃЎвбжЊPQЃН![]() ЃЌЧѓЕуPЕФзјБъЃЎ
ЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
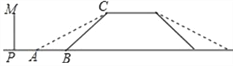
ЁОЬтФПЁПФГЕиЕФвЛзљШЫааЬьЧХШчЭМЫљЪОЃЌЬьЧХИпЮЊ6УзЃЌЦТУцBCЕФЦТЖШЮЊ1ЃК1ЃЌЮЊСЫЗНБуааШЫЭЦГЕЙ§ЬьЧХЃЌгаЙиВПУХОіЖЈНЕЕЭЦТЖШЃЌЪЙаТЦТУцЕФЦТЖШЮЊ1ЃК![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓаТЦТУцЕФЦТНЧЁЯCABЕФЖШЪ§ЃЛ
ЃЈ2ЃЉдЬьЧХЕзВПе§ЧАЗН8УзДІЃЈPBЕФГЄЃЉЕФЮФЛЏЧНPMЪЧЗёашвЊВ№Г§ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌМКжЊЕуAЪЧЫЋЧњЯпy=kx-1(k>0)ЩЯЕФвЛИіЖЏЕуЃЌСЌAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊБпзїЕШБпЁїABCЃЌЕуCдкЕкЫФЯѓЯоЃЎЫцзХЕуAЕФдЫЖЏЃЌЕуCЕФЮЛжУвВВЛЖЯБфЛЏЃЌЕЋЕуCЪМжедкЫЋЧњЯпy=mx-1(m<0)ЩЯдЫЖЏЃЌдђmгыkЕФЙиЯЕЪЧЃЈ ЃЉ

A. m= -kB. m=![]() kC. m= -2kD. m= -3k
kC. m= -2kD. m= -3k
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com