
 如图,某农场有一块四边形ABCD的空地,其各边中点分别是E、F、G、H,测得对角线AC=BD=12米,现想用篱笆围成四边形EFGH的场地,则需用的篱笆总长度是( )
如图,某农场有一块四边形ABCD的空地,其各边中点分别是E、F、G、H,测得对角线AC=BD=12米,现想用篱笆围成四边形EFGH的场地,则需用的篱笆总长度是( )| A. | 12米 | B. | 24米 | C. | 36米 | D. | 48米 |
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
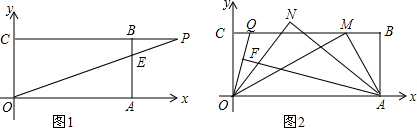
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将矩形纸片ABCD沿直线AE折叠,点B恰好落在线段CD的中点F上,点G是线段AF上一动点(不与A,F重合),点G过GH⊥AB,垂足为H,将矩形沿直线GH翻折,点A恰好落在线段BH上点A′处.若AB长为8,则当△A′GE为直角三角形时,AH的长为$\frac{24-8\sqrt{3}}{3}$.
如图,将矩形纸片ABCD沿直线AE折叠,点B恰好落在线段CD的中点F上,点G是线段AF上一动点(不与A,F重合),点G过GH⊥AB,垂足为H,将矩形沿直线GH翻折,点A恰好落在线段BH上点A′处.若AB长为8,则当△A′GE为直角三角形时,AH的长为$\frac{24-8\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P是矩形ABCD的边AD上一动点,矩形的两条 边长AB、BC分别为8和15,则点P到矩形的两条对角线AC和BD的距离之和为$\frac{120}{17}$.
如图,点P是矩形ABCD的边AD上一动点,矩形的两条 边长AB、BC分别为8和15,则点P到矩形的两条对角线AC和BD的距离之和为$\frac{120}{17}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com