
 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.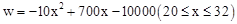 ;(2)当销售单价定为32元时,每月可获得最大利润,最大利润是2160元;(3)3600.
;(2)当销售单价定为32元时,每月可获得最大利润,最大利润是2160元;(3)3600. .
.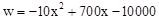 的图象的对称轴是直线
的图象的对称轴是直线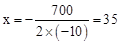 ,
,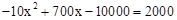 ,解这个方程得:x1=30,x2=40。
,解这个方程得:x1=30,x2=40。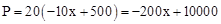 ,
,

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
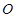 点表示喷水池的水面中心,
点表示喷水池的水面中心,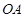 表示喷水柱子,水流从
表示喷水柱子,水流从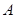 点喷出,按如图所示的直角坐标系,每一股水流在空中的路线可以用
点喷出,按如图所示的直角坐标系,每一股水流在空中的路线可以用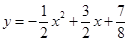 来描述,那么水池的半径至少要 米,才能使喷出的水流不致落到池外。
来描述,那么水池的半径至少要 米,才能使喷出的水流不致落到池外。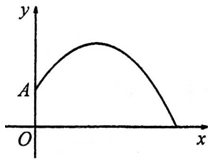
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:
(a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:| x | … | ―1 | 0 | 3 | … |
 | … | 0 |  | 0 | … |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
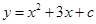 过两点(m,0)、(n,0),且
过两点(m,0)、(n,0),且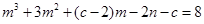 ,抛物线于双曲线
,抛物线于双曲线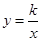 (x>0)的交点为(1,d).
(x>0)的交点为(1,d).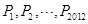 都在双曲线
都在双曲线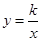 (x>0)上,它们的横坐标分别为
(x>0)上,它们的横坐标分别为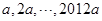 ,O为坐标原点,记
,O为坐标原点,记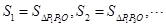 ,点Q在双曲线
,点Q在双曲线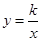 (x<0)上,过Q作QM⊥y轴于M,记
(x<0)上,过Q作QM⊥y轴于M,记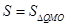 。
。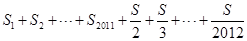 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com