
【题目】如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )

A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
【答案】D
【解析】
试题分析:根据三角形的内角和等于180°求出∠ABC+∠ACB=120°,再根据角平分线的性质求出∠OBC+∠OCB=60°,然后利用三角形的内角和等于180°列式计算即可求出∠BOC的度数;
连接OA,作OF⊥AB于点F,OG⊥AC于点G,OH⊥BC于点H,根据角平分线上的点到角的两边的距离相等可得OF=OG=OH,从而可得△BOF和△BOH全等,△COG和△COH全等,根据全等三角形对应边相等可得BH=BF,CH=CG,再根据四边形的内角和求出∠FOG=120°,根据对顶角相等求出∠EOD=120°,然后推出∠EOF=∠DOG,再利用“角边角”证明△EOF和△DOG全等,根据全等三角形对应边相等可得EF=DG,OD=OE,即可判定出B、C选项都正确,根据等角对等边的性质,只有∠ABC=∠ACB时才能得到OB=OC,所以D选项错误.
解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣60°=120°,
∵△ABC的两条角平分线BD、CE交于O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣![]() (∠ABC+∠ACB)=120°,故A选项正确;
(∠ABC+∠ACB)=120°,故A选项正确;
如图,连接OA,作OF⊥AB于点F,OG⊥AC于点G,OH⊥BC于点H,
∵△ABC的两条角平分线BD、CE交于O,
∴OF=OG=OH,
利用“HL”可得△BOF≌△BOH,△COG≌△COH,
∴BH=BF,CH=CG,
在四边形AFOG中,∠FOG=360°﹣60°﹣90°×2=120°,
∴DOG=∠FOG﹣∠DOF=120°﹣∠DOF,
又∵∠EOD=∠BOC=120°,
∴∠EOF=∠EOD﹣∠DOF=120°﹣∠DOF,
∴∠EOF=∠DOG,
在△EOF和△DOG中,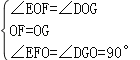 ,
,
∴△EOF≌△DOG(ASA),
∴EF=DG,OD=OE,故C选项正确;
∴BC=BH+CH=BF+CG=BE+EF+CD﹣DG=BE+CD,
即BC=BE+CD,故B选项正确;
只有当∠ABC=∠ACB时,∵△ABC的两条角平分线BD、CE交于O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC=∠OCB,
∴OB=OC,
而本题无法得到∠ABC=∠ACB,
所以,OB=OC不正确,故D选项错误.
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法中:①一个有理数不是正数就是负数;②射线AB和射线BA是同一条射线;③0的相反数是它本身;④两点之间,线段最短,正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N若点M的横坐标为m,请用m的代数式表示MN的长。
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年下半年开始,不同品牌的共享单车出现在城市的大街小巷.现已知A品牌共享单车计费方式为:初始骑行单价为1元/半小时,不足半小时按半小时计算.内设邀请机制,每邀请一位好友注册认证并充值押金成功,双方骑行单价均降价0.1元/半小时,骑行单价最低可降至0.1元/半小时(比如,某用户邀请了3位好友,则骑行单价为0.7元/半小时).B品牌共享单车计费方式为:0.5元/半小时,不足半小时按半小时计算.
(1)某用户准备选择A品牌共享单车使用,设该用户邀请好友x名(x为整数,x≥0),该用户的骑行单价为y元/半小时.请写出y关于x的函数解析式.
(2)若有A,B两种品牌的共享单车各一辆供某用户一人选择使用,请你根据该用户已邀请好友的人数,给出经济实惠的选择建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰部角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1 m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com