
 如图,在直角坐标系中,A、B的坐标分别为(4,0),(0,2),将线段AB向上平移m个单位得到A′B′,如果△OA′B′为等腰三角形,那么m的值为2或3或2$\sqrt{5}$-2.
如图,在直角坐标系中,A、B的坐标分别为(4,0),(0,2),将线段AB向上平移m个单位得到A′B′,如果△OA′B′为等腰三角形,那么m的值为2或3或2$\sqrt{5}$-2. 分析 根据A、B的坐标分别为(4,0),(0,2),得到OA=4,OB=2,根据勾股定理得到AB=2$\sqrt{5}$,由将线段AB向上平移m个单位得到A′B′,得到A′B′=2$\sqrt{5}$,根据△OA′B′为等腰三角形,①当OB′=A′B′=2$\sqrt{5}$时,②当OA′=A′B′=2$\sqrt{5}$时,③当OB′=A′O=2+m时,分别求得m的值即可.
解答 解:∵A、B的坐标分别为(4,0),(0,2),
∴OA=4,OB=2,
∴AB=2$\sqrt{5}$,
∵将线段AB向上平移m个单位得到A′B′,
∴A′B′=2$\sqrt{5}$,
∵△OA′B′为等腰三角形,
∴①当OB′=A′B′=2$\sqrt{5}$时,
∴m=BB′=2$\sqrt{5}$-2;
②当OA′=A′B′=2$\sqrt{5}$时,m=AA′=2,
③当OB′=A′O=2+m时,
∴2+m=$\sqrt{{4}^{2}+{m}^{2}}$,
∴m=3,
综上所述,如果△OA′B′为等腰三角形,那么m的值为2或3或2$\sqrt{5}$-2.
故答案为:2或3或2$\sqrt{5}$-2.
点评 此题主要考查了坐标与图形的变化--平移,关键是掌握点的坐标的变化规律.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
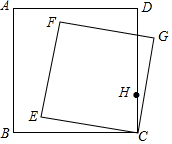 如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )
如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{2}}{5}$ | C. | $\frac{\sqrt{2}}{7}$ | D. | $\frac{1}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
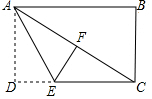 如图,在矩形ABCD中,将△ADE沿AE折叠,点D刚好落在对角线AC上的F点.
如图,在矩形ABCD中,将△ADE沿AE折叠,点D刚好落在对角线AC上的F点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
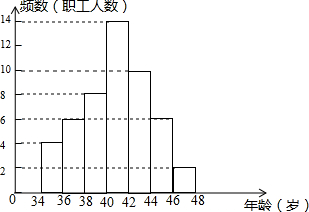 如图是某单位职工年龄(取正整数)的频数分布直方图(每组数据含最小值,不含最大值),则职工人数最多年龄段的职工人数占总人数的百分比为28%.
如图是某单位职工年龄(取正整数)的频数分布直方图(每组数据含最小值,不含最大值),则职工人数最多年龄段的职工人数占总人数的百分比为28%.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
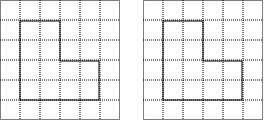 如图所示,在正方形网格中,要求用一条直线将其分成面积相等的两部分,请你设计两种不同的分割方案(用铅笔画图,不写画法,仅用有刻度的直尺,保留作图痕迹或必要的文字说明).
如图所示,在正方形网格中,要求用一条直线将其分成面积相等的两部分,请你设计两种不同的分割方案(用铅笔画图,不写画法,仅用有刻度的直尺,保留作图痕迹或必要的文字说明).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com