
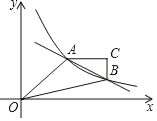
【题目】如图,在平面直角坐标系中,一次函数y=﹣![]() x+3的图象与反比例函数y=
x+3的图象与反比例函数y=![]() (x>0,k是常数)的图象交于A(a,2),B(4,b)两点.
(x>0,k是常数)的图象交于A(a,2),B(4,b)两点.
(1)求反比例函数的表达式;
(2)点C是第一象限内一点,连接AC,BC,使AC∥x轴,BC∥y轴,连接OA,OB.若点P在y轴上,且△OPA的面积与四边形OACB的面积相等,求点P的坐标.
【答案】(1) 反比例函数的表达式为y=![]() (x>0);(2) 点P的坐标为(0,4)或(0,﹣4)
(x>0);(2) 点P的坐标为(0,4)或(0,﹣4)
【解析】
(1)根据点A(a,2),B(4,b)在一次函数y=﹣![]() x+3的图象上求出a、b的值,得出A、B两点的坐标,再运用待定系数法解答即可;
x+3的图象上求出a、b的值,得出A、B两点的坐标,再运用待定系数法解答即可;
(2)延长CA交y轴于点E,延长CB交x轴于点F,构建矩形OECF,根据S四边形OACB=S矩形OECF﹣S△OAE﹣S△OBF,设点P(0,m),根据反比例函数的几何意义解答即可.
(1)∵点A(a,2),B(4,b)在一次函数y=﹣![]() x+3的图象上,
x+3的图象上,
∴﹣![]() a+3=2,b=﹣
a+3=2,b=﹣![]() ×4+3,
×4+3,
∴a=2,b=1,
∴点A的坐标为(2,2),点B的坐标为(4,1),
又∵点A(2,2)在反比例函数y=![]() 的图象上,
的图象上,
∴k=2×2=4,
∴反比例函数的表达式为y=![]() (x>0);
(x>0);
(2)延长CA交y轴于点E,延长CB交x轴于点F,
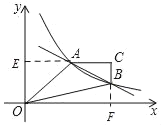
∵AC∥x轴,BC∥y轴,
则有CE⊥y轴,CF⊥x轴,点C的坐标为(4,2)
∴四边形OECF为矩形,且CE=4,CF=2,
∴S四边形OACB=S矩形OECF﹣S△OAE﹣S△OBF
=2×4﹣![]() ×2×2﹣
×2×2﹣![]() ×4×1
×4×1
=4,
设点P的坐标为(0,m),
则S△OAP=![]() ×2|m|=4,
×2|m|=4,
∴m=±4,
∴点P的坐标为(0,4)或(0,﹣4).


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
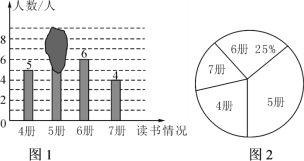
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形统计图(如图1)和不完整的扇形图(如图2),其中条形统计图被墨迹遮盖了一部分.
(1)求条形统计图中被遮盖的数,并写出册数的中位数;
(2)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没有改变,则最多补查了____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
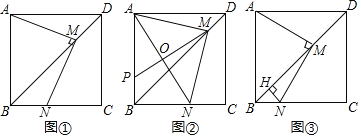
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点
上的一个动点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)如图①,求证:![]() ;
;
(2)如图②,连接![]() 为
为![]() 的中点,
的中点,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 和
和![]() 的长;
的长;
(3)如图③,过点![]() 作
作![]() 于
于![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料, 每瓶进价为![]() 元,当每瓶售价
元,当每瓶售价![]() 元时,日均销售量
元时,日均销售量![]() 瓶.经市场调查表明,每瓶售价每增加
瓶.经市场调查表明,每瓶售价每增加![]() 元,日均销售量减少
元,日均销售量减少![]() 瓶.
瓶.
(1)当每瓶售价为![]() 元时,日均销售量为 瓶;
元时,日均销售量为 瓶;
(2)当每瓶售价为多少元时,所得日均总利润为![]() 元;
元;
(3)当每瓶售价为多少元时,所得日均总利润最大?最大日均总利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,与过
,与过![]() 点的直线相交于另一点
点的直线相交于另一点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .
.
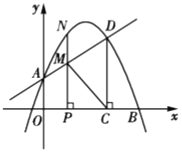
(1)求抛物线的解析式.
(2)点![]() 是
是![]() 轴正半轴上的一个动点,过点
轴正半轴上的一个动点,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
①若点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
②设![]() 的长为
的长为![]() ,是否存在
,是否存在![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
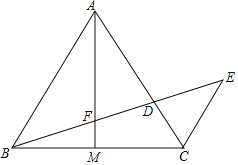
【题目】如图,△ABC中,AB=AC,AM为BC边的中线,点D在边AC上,联结BD交AM于点F,延长BD至点E,使得![]() =
=![]() ,联结CE.
,联结CE.
求证:(1)∠ECD=2∠BAM;
(2)BF是DF和EF的比例中项.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xoy中,对于点P(x,y) 和Q(x, y′) .给出如下定义:若 ![]() ,则称点Q 为点P 的“可控变点” . 例如:点(1,2)的可控变点为点(1,2),点(-1,3)的可控变点为点(-1,-3).
,则称点Q 为点P 的“可控变点” . 例如:点(1,2)的可控变点为点(1,2),点(-1,3)的可控变点为点(-1,-3).
(1)点(-6,-3)的可控变点坐标为________.
(2)若点P在函数y=-x2+16的图象上,其可控变点Q的纵坐标y′是7,求可控变点Q的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com