
ΓΨΧβΡΩΓΩΥφΉ≈Ψ≠ΦΟΩλΥΌΖΔ’ΙΘ§ΜΖΨ≥Έ Χβ‘Ϋά¥‘Ϋ ήΒΫ»ΥΟ«ΒΡΙΊΉΔΘ°Ρ≥–ΘΈΣΝΥΝΥΫβΫΎΡήΦθ≈≈ΓΔά§ΜχΖ÷άύΒ»÷Σ ΕΒΡΤ’ΦΑ«ιΩωΘ§ΥφΜζΒς≤ιΝΥ≤ΩΖ÷―ß…ζΘ§Βς≤ιΫαΙϊΖ÷ΈΣΓΑΖ«≥ΘΝΥΫβΓ±ΓΑΝΥΫβΓ±ΓΑΝΥΫβΫœ…ΌΓ±ΓΑ≤ΜΝΥΫβΓ±ΥΡάύΘ§≤ΔΫΪΫαΙϊΜφ÷Τ≥…“‘œ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΗυΨίΆ≥ΦΤΆΦΜΊ¥πœ¬Ν–Έ ΧβΘΚ
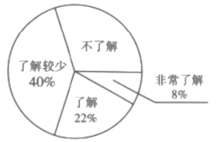
Θ®1Θ©±Ψ¥ΈΒς≤ιΒΡ―ß…ζΙ≤”–___________»ΥΘ§ΙάΦΤΗΟ–Θ![]() Οϊ―ß…ζ÷–ΓΑ≤ΜΝΥΫβΓ±ΒΡ»Υ ΐ «__________»ΥΘΜ
Οϊ―ß…ζ÷–ΓΑ≤ΜΝΥΫβΓ±ΒΡ»Υ ΐ «__________»ΥΘΜ
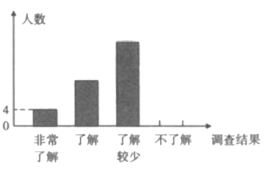
Θ®2Θ©ΫΪΧθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©ΓΑΖ«≥ΘΝΥΫβΓ±ΒΡ![]() »Υ÷–”–
»Υ÷–”–![]() Θ§
Θ§![]() ΝΫΟϊΡ–…ζΘ§
ΝΫΟϊΡ–…ζΘ§![]() Θ§
Θ§![]() ΝΫΟϊ≈°…ζΘ§»τ¥”÷–ΥφΜζ≥ι»ΓΝΫ»Υ»Ξ≤ΈΦ”ΜΖ±Θ÷Σ ΕΨΚ»ϋΘ§«κ”ΟΜ≠ ςΉ¥ΆΦΜρΝ–±μΒΡΖΫΖ®Θ§«σ«ΓΚΟ≥ιΒΫ
ΝΫΟϊ≈°…ζΘ§»τ¥”÷–ΥφΜζ≥ι»ΓΝΫ»Υ»Ξ≤ΈΦ”ΜΖ±Θ÷Σ ΕΨΚ»ϋΘ§«κ”ΟΜ≠ ςΉ¥ΆΦΜρΝ–±μΒΡΖΫΖ®Θ§«σ«ΓΚΟ≥ιΒΫ![]() ΟϊΡ–…ζΒΡΗ≈¬ Θ°
ΟϊΡ–…ζΒΡΗ≈¬ Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©50Θ§600ΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©ΦϊΫβΈωΘ§![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©”ΟΓΑΖ«≥ΘΝΥΫβΓ±ΒΡ»Υ ΐ≥ΐ“‘ΤδΕ‘”ΠΑΌΖ÷±»Ω…ΒΟΉή»Υ ΐΘ§”Ο1Φθ»ΞΤδΥϊΥυ’ΦΒΡΑΌΖ÷±»Ω…ΒΟΓΑ≤ΜΝΥΫβΓ±ΒΡ―ß…ζΥυ’ΦΑΌΖ÷±»Θ§”Ο2000≥Υ“‘ΓΑ≤ΜΝΥΫβΓ±ΒΡ―ß…ζΥυ’ΦΑΌΖ÷±»Φ¥Ω…ΒΟΓΑ≤ΜΝΥΫβΓ±ΒΡ―ß…ζ»Υ ΐΘΜ
Θ®2Θ©œ»«σ≥ωΓΑ≤ΜΝΥΫβΓ±ΒΡ»Υ ΐΘ§‘Ό≤Ι≥δΧθ–ΈΆ≥ΦΤΆΦΦ¥Ω…ΘΜ
Θ®3Θ©ΗυΨίΧβ“βΜ≠≥ω±μΗώΘ§Ω…ΒΟ“ΜΙ≤12÷÷≥ι»Γ«ιΩωΘ§«ΓΚΟ≥ιΒΫ2ΟϊΡ–…ζΒΡ«ιΩω”–2÷÷Θ§‘Όάϊ”ΟΗ≈¬ ΙΪ ΫΦΤΥψΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©±Ψ¥ΈΒς≤ιΒΡ―ß…ζΉή»Υ ΐΈΣ![]() »ΥΘΜΓΑ≤ΜΝΥΫβΓ±ΒΡ―ß…ζΥυ’ΦΑΌΖ÷±»ΈΣ
»ΥΘΜΓΑ≤ΜΝΥΫβΓ±ΒΡ―ß…ζΥυ’ΦΑΌΖ÷±»ΈΣ![]() Θ§
Θ§
![]() ΙάΦΤΗΟ–Θ
ΙάΦΤΗΟ–Θ![]() Οϊ―ß…ζ÷–ΓΑ≤ΜΝΥΫβΓ±ΒΡ»Υ ΐ‘Φ”–
Οϊ―ß…ζ÷–ΓΑ≤ΜΝΥΫβΓ±ΒΡ»Υ ΐ‘Φ”–![]() Θ®»ΥΘ©
Θ®»ΥΘ©
Θ®2Θ©30%ΓΝ50=15Θ®»ΥΘ©
»γœ¬ΆΦ
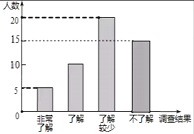
Θ®3Θ©Ν–±μ»γœ¬Θ§”…±μΩ…÷ΣΙ≤”–![]() ÷÷Ω…ΡήΒΡΫαΙϊΘ§«ΓΚΟ≥ιΒΫ
÷÷Ω…ΡήΒΡΫαΙϊΘ§«ΓΚΟ≥ιΒΫ![]() ΟϊΡ–…ζΒΡΫαΙϊ”–
ΟϊΡ–…ζΒΡΫαΙϊ”–![]() ΗωΘ§
ΗωΘ§
![]() Θ®«ΓΚΟ≥ιΒΫ
Θ®«ΓΚΟ≥ιΒΫ![]() ΟϊΡ–…ζΘ©
ΟϊΡ–…ζΘ©![]()
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
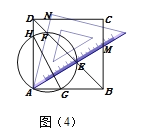
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΝβ–ΈABCD÷–Θ§AB=BDΘ§ΒψEΓΔFΖ÷±π‘ΎBCΓΔCD…œΘ§«“BE=CFΘ§Ν§Ϋ”BFΓΔDEΫΜ”ΎΒψMΘ§―”≥ΛEDΒΫH ΙDH=BMΘ§Ν§Ϋ”AMΘ§AHΘ§‘ρ“‘œ¬ΥΡΗωΫα¬έΘΚ
ΔΌΓςBDFΓ’ΓςDCEΘΜΔΎΓœBMD=120ΓψΘΜΔέΓςAMH «Β»±Ώ»ΐΫ«–ΈΘΜΔήSΥΡ±Ώ–ΈABCD= ![]() AM2Θ°
AM2Θ°
Τδ÷–’ΐ»ΖΫα¬έΒΡΗω ΐ «Θ® Θ©
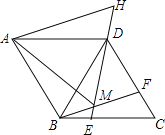
A. 1 B. 2 C. 3 D. 4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝάμΫβΘ§≤ΔΜΊ¥πΈ ΧβΘΚ
»τx1Θ§x2 «ΖΫ≥Χax2+bx+cΘΫ0ΒΡΝΫΗω Β ΐΗυΘ§‘ρ”–ax2+bx+cΘΫaΘ®x©¹x1Θ©Θ®x©¹x2Θ©Θ°Φ¥ax2+bx+cΘΫax2©¹aΘ®x1+x2Θ©x+ax1x2Θ§”Ύ «bΘΫ©¹aΘ®x1+x2Θ©Θ§cΘΫax1x2Θ°”…¥ΥΩ…ΒΟ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΒΡΗυ”κœΒ ΐΙΊœΒΘΚx1+x2ΘΫ©¹![]() Θ§x1x2ΘΫ
Θ§x1x2ΘΫ![]() Θ°’βΨΆ «Έ“Ο«÷ΎΥυ÷ή÷ΣΒΡΈΛ¥οΕ®άμΘ°
Θ°’βΨΆ «Έ“Ο«÷ΎΥυ÷ή÷ΣΒΡΈΛ¥οΕ®άμΘ°
Θ®1Θ©“―÷ΣmΘ§n «ΖΫ≥Χx2©¹x©¹100ΘΫ0ΒΡΝΫΗω Β ΐΗυΘ§≤ΜΫβΖΫ≥Χ«σm2+n2ΒΡ÷ΒΘΜ
Θ®2Θ©»τx1Θ§x2Θ§x3Θ§ «ΙΊ”ΎxΒΡΖΫ≥ΧxΘ®x©¹2Θ©2ΘΫtΒΡ»ΐΗω Β ΐΗυΘ§«“x1ΘΦx2ΘΦx3ΘΜ
ΔΌx1x2+x2x3+x3x1ΒΡ÷ΒΘΜΔΎ«σx3©¹x1ΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ‘”ΎΤΫΟφΡΎ![]() ΚΆ
ΚΆ![]() Άβ“ΜΒψ
Άβ“ΜΒψ![]() Θ§»τΙΐΒψ
Θ§»τΙΐΒψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κ
”κ![]() ”–ΝΫΗω≤ΜΆ§ΒΡΙΪΙ≤Βψ
”–ΝΫΗω≤ΜΆ§ΒΡΙΪΙ≤Βψ![]() Θ§Βψ
Θ§Βψ![]() ΈΣ÷±œΏ
ΈΣ÷±œΏ![]() …œΒΡΝμ“ΜΒψΘ§«“¬ζΉψ
…œΒΡΝμ“ΜΒψΘ§«“¬ζΉψ![]() (»γΆΦ1Υυ Ψ)Θ§‘ρ≥ΤΒψ
(»γΆΦ1Υυ Ψ)Θ§‘ρ≥ΤΒψ![]() «Βψ
«Βψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΟή«–ΒψΘ°
ΒΡΟή«–ΒψΘ°
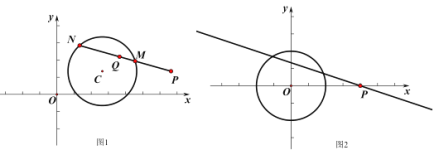
“―÷Σ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§
÷–Θ§ ![]() ΒΡΑκΨΕΈΣ2Θ§Βψ
ΒΡΑκΨΕΈΣ2Θ§Βψ![]() Θ°
Θ°
(1)‘ΎΒψ![]()
![]() ÷–Θ§ «Βψ
÷–Θ§ «Βψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΟή«–ΒψΒΡΈΣ__________Θ°
ΒΡΟή«–ΒψΒΡΈΣ__________Θ°
(2)…η÷±œΏ![]() ΖΫ≥ΧΈΣ
ΖΫ≥ΧΈΣ![]() Θ§»γΆΦ2Υυ ΨΘ§
Θ§»γΆΦ2Υυ ΨΘ§
ΔΌ![]() ±Θ§«σ≥ωΒψ
±Θ§«σ≥ωΒψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΟή«–Βψ
ΒΡΟή«–Βψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
ΔΎ![]() ΒΡ‘≤–ΡΈΣ
ΒΡ‘≤–ΡΈΣ![]() Θ§ΑκΨΕΈΣ2Θ§»τ
Θ§ΑκΨΕΈΣ2Θ§»τ![]() …œ¥φ‘ΎΒψ
…œ¥φ‘ΎΒψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΟή«–ΒψΘ§÷±Ϋ”–¥≥ω
ΒΡΟή«–ΒψΘ§÷±Ϋ”–¥≥ω![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ‘”ΎΤΫΟφΡΎ![]() ΚΆ
ΚΆ![]() Άβ“ΜΒψ
Άβ“ΜΒψ![]() Θ§»τΙΐΒψ
Θ§»τΙΐΒψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κ
”κ![]() ”–ΝΫΗω≤ΜΆ§ΒΡΙΪΙ≤Βψ
”–ΝΫΗω≤ΜΆ§ΒΡΙΪΙ≤Βψ![]() Θ§Βψ
Θ§Βψ![]() ΈΣ÷±œΏ
ΈΣ÷±œΏ![]() …œΒΡΝμ“ΜΒψΘ§«“¬ζΉψ
…œΒΡΝμ“ΜΒψΘ§«“¬ζΉψ![]() (»γΆΦ1Υυ Ψ)Θ§‘ρ≥ΤΒψ
(»γΆΦ1Υυ Ψ)Θ§‘ρ≥ΤΒψ![]() «Βψ
«Βψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΟή«–ΒψΘ°
ΒΡΟή«–ΒψΘ°
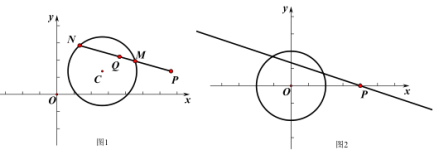
“―÷Σ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§
÷–Θ§ ![]() ΒΡΑκΨΕΈΣ2Θ§Βψ
ΒΡΑκΨΕΈΣ2Θ§Βψ![]() Θ°
Θ°
(1)‘ΎΒψ![]()
![]() ÷–Θ§ «Βψ
÷–Θ§ «Βψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΟή«–ΒψΒΡΈΣ__________Θ°
ΒΡΟή«–ΒψΒΡΈΣ__________Θ°
(2)…η÷±œΏ![]() ΖΫ≥ΧΈΣ
ΖΫ≥ΧΈΣ![]() Θ§»γΆΦ2Υυ ΨΘ§
Θ§»γΆΦ2Υυ ΨΘ§
ΔΌ![]() ±Θ§«σ≥ωΒψ
±Θ§«σ≥ωΒψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΟή«–Βψ
ΒΡΟή«–Βψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
ΔΎ![]() ΒΡ‘≤–ΡΈΣ
ΒΡ‘≤–ΡΈΣ![]() Θ§ΑκΨΕΈΣ2Θ§»τ
Θ§ΑκΨΕΈΣ2Θ§»τ![]() …œ¥φ‘ΎΒψ
…œ¥φ‘ΎΒψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΟή«–ΒψΘ§÷±Ϋ”–¥≥ω
ΒΡΟή«–ΒψΘ§÷±Ϋ”–¥≥ω![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
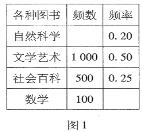
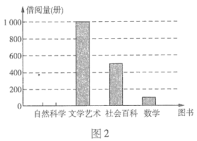
ΓΨΧβΡΩΓΩΡ≥÷–―ßΆΦ ιΙίΫΪΆΦ ιΖ÷ΈΣΉ‘»ΜΩΤ―ßΓΔΈΡ―ß“’ θΓΔ…γΜαΑΌΩΤΓΔ ΐ―ßΥΡάύ‘ΎΓΑΕΝ ι‘¬Γ±ΜνΕ·÷–Θ§ΈΣΝΥΝΥΫβΆΦ ιΒΡΫη‘Ρ«ιΩωΘ§ΆΦ ιΙήάμ‘±Ε‘±Ψ‘¬ΗςάύΆΦ ιΒΡΫη‘ΡΫχ––ΝΥΆ≥ΦΤΘ§ΆΦ1ΚΆΆΦ2 «ΆΦ ιΙήάμ‘±Ά®Ιΐ≤…Φ· ΐΨίΚσΜφ÷ΤΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΤΒ¬ Ζ÷≤Φ±μ”κΤΒ ΐΖ÷≤ΦΧθ–ΈΆΦΘ°«κΡψΗυΨίΆΦ±μ÷–ΧαΙ©ΒΡ–≈œΔΘ§Ϋβ¥π“‘œ¬Έ ΧβΘΚ
Θ®1Θ©Χν≥δΆΦ1ΤΒ¬ Ζ÷≤Φ±μ÷–ΒΡΩ’ΗώΘΜ
Θ®2Θ©‘ΎΆΦ2÷–Θ§ΫΪ±μ ΨΓΑΉ‘»ΜΩΤ―ßΓ±ΒΡ≤ΩΖ÷≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©»τΗΟ―ß–Θ¥ρΥψ≤…ΙΚ“ΜΆρ≤αΆΦ ιΘ§«κΡψΙάΥψΓΑ ΐ―ßΓ±άύΆΦ ι”Π≤…ΙΚΕύ…Ό≤αΫœΚœ ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕΰ¥ΈΚ· ΐ![]() …œ≤ΩΖ÷ΒψΒΡΚαΉχ±ξx”κΉίΉχ±ξyΒΡΕ‘”Π÷Β»γœ¬±μΘΚ
…œ≤ΩΖ÷ΒψΒΡΚαΉχ±ξx”κΉίΉχ±ξyΒΡΕ‘”Π÷Β»γœ¬±μΘΚ
x | Γ≠ |
|
| 0 | 1 | 2 | 3 | Γ≠ |
y | Γ≠ | 3 |
| 0 |
| 0 | m | Γ≠ |

Θ®1Θ©÷±Ϋ”–¥≥ω¥ΥΕΰ¥ΈΚ· ΐΒΡΕ‘≥Τ÷α ΘΜ
Θ®2Θ©«σbΒΡ÷ΒΘΜ
Θ®3Θ©÷±Ϋ”–¥≥ω±μ÷–ΒΡm÷ΒΘ§m= ΘΜ
Θ®4Θ©‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§Μ≠≥ω¥ΥΕΰ¥ΈΚ· ΐΒΡΆΦœσΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
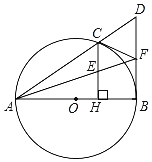
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΒψC «“‘ABΈΣ÷±ΨΕΒΡΓ―O…œ“ΜΒψΘ§CHΓΆAB”ΎΒψHΘ§ΙΐΒψBΉςΓ―OΒΡ«–œΏΫΜ÷±œΏAC”ΎΒψDΘ§ΒψEΈΣCHΒΡ÷–ΒψΘ§Ν§Ϋ”AE≤Δ―”≥ΛΫΜBD”ΎΒψFΘ§Ν§Ϋ”CFΘ°
Θ®1Θ©«σ÷ΛΘΚCFΘΫBFΘΜ
Θ®2Θ©«σ÷ΛΘΚCF «Γ―OΒΡ«–œΏΘΜ
Θ®3Θ©»τFBΘΫFEΘΫ3Θ§«σΓ―OΒΡΑκΨΕΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ ΐ―ß―ßœΑ–ΓΉιΓΑ¬Ϋ‘¬Μ‘ΜΆΓ±ΉνΫϋ’ΐ‘ΎΫχ––ΦΗΚΈΆΦ–ΈΉιΚœΈ ΧβΒΡ―–ΨΩΘ°»œ’φ―–ΕΝ“‘œ¬ΥΡΗωΤ§ΕΈΘ§≤ΔΜΊ¥πΈ ΧβΘ°
Θ®Τ§Εœ“ΜΘ©–Γ¬ΫΥΒΘΚΫΪ“ΜΩιΉψΙΜ¥σΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«Αε÷Ο”Ύ“ΜΗω’ΐΖΫ–Έ÷–Θ§÷±Ϋ«ΕΞΒψ”κΕ‘Ϋ«œΏΫΜΒψO÷ΊΚœΘ§‘ΎΉΣΕ·»ΐΫ«ΑεΒΡΙΐ≥Χ÷–Έ“ΖΔœ÷Ρ≥–©œΏΕΈ÷°Φδ¥φ‘Ύ»ΖΕ®ΒΡ ΐΝΩΙΊœΒΘ°
»γΆΦΘ®1Θ©Θ§»τ»ΐΫ«ΑεΝΫΧθ÷±Ϋ«±ΏΒΡΆβ―ΊΖ÷±πΫΜ’ΐΖΫ–ΈΒΡ±ΏABΓΔBC”ΎΒψMΓΔNΘ§‘ρΔΌOMΘΪON=MBΘΪNBΘΜΔΎ![]() Θ°
Θ°
«κΡψ≈–ΕœΥϊΒΡ≤¬œκ «Ζώ’ΐ»ΖΘΩ≤Δ÷ΛΟςΡψ»œΈΣ’ΐ»ΖΒΡ≤¬œκΘ°
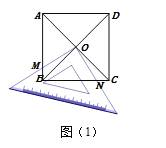
Θ®Τ§ΕœΕΰΘ©–Γ‘¬ΥΒΘΚΫΪ»ΐΫ«Αε÷–“ΜΗω45ΓψΫ«ΒΡΕΞΒψΚΆ’ΐΖΫ–ΈΒΡ“ΜΗωΕΞΒψ÷ΊΚœΖ≈÷ΟΘ§ ΙΒΟ’βΗωΫ«ΒΡΝΫΧθ±Ώ”κ’ΐΖΫ–ΈΒΡ“ΜΉιΝΎ±Ώ”–ΫΜΒψΘ°
»γΆΦΘ®2Θ©Θ§»τ“‘AΈΣΕΞΒψΒΡ45ΓψΫ«ΒΡΝΫ±ΏΖ÷±πΫΜ’ΐΖΫ–ΈΒΡ±ΏBCΓΔCD”ΎΒψMΓΔNΘ§ΫΜΕ‘Ϋ«œΏBD”ΎΒψEΓΔFΘ°Έ“ΖΔœ÷ΘΚBE2ΘΪDE2=2AE2Θ§÷Μ“ΣΉΦ»Ζ–ΐΉΣΆΦΘ®2Θ©÷–ΒΡ“ΜΗω»ΐΫ«–ΈΨΆΡή÷ΛΟς’βΗωΫα¬έΘ°
«κΡψ–¥≥ω–Γ‘¬ΥυΥΒΒΡΨΏΧεΒΡ–ΐΉΣΖΫ ΫΘΚ______________________Θ°
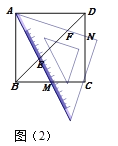
Θ®Τ§Εœ»ΐΘ©–ΓΜ‘ΥΒΘΚΫΪ»ΐΫ«ΑεΒΡ“ΜΗω45ΓψΫ«Ζ≈÷Ο‘Ύ’ΐΖΫ–ΈΒΡΆβ≤ΩΘ§Ά§ ±Ϋ«ΒΡΝΫ±Ώ«ΓΚΟΨ≠Ιΐ’ΐΖΫ–ΈΝΫΗωœύΝΎΒΡΕΞΒψΘ°
»γΆΦΘ®3Θ©Θ§…ηΕΞΒψΈΣEΒΡ45ΓψΫ«ΈΜ”Ύ’ΐΖΫ–ΈΒΡ±ΏAD…œΖΫΘ§’βΗωΫ«ΒΡΝΫ±ΏΖ÷±πΨ≠ΙΐΒψBΓΔCΘ§Ν§Ϋ”EAΘ§EDΘ°Ρ«Ο¥œΏΕΈEBΓΔECΓΔED“≤¥φ‘Ύ»ΖΕ®ΒΡ ΐΝΩΙΊœΒΘΚ(EBΘΪED)2=2EC2Θ°
«κΡψ÷ΛΟς’βΗωΫα¬έΘ°
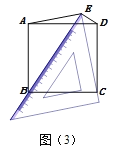
Θ®Τ§ΕœΥΡΘ©–ΓΜΆΥΒΘΚ‘ΎΆΦΘ®2Θ©÷–Θ§Ής“ΜΗωΙΐΒψAΓΔEΓΔFΒΡ‘≤Θ§ΫΜ’ΐΖΫ–ΈΒΡ±ΏABΓΔAD”ΎΒψGΓΔHΘ§»γΆΦΘ®4Θ©Υυ ΨΘ°Ρψ÷ΣΒάœΏΕΈDHΓΔHGΓΔGB»ΐ’Ώ÷°ΦδΒΡΙΊœΒ¬πΘΩ«κ÷±Ϋ”–¥≥ωΫα¬έΘΚ________________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com