
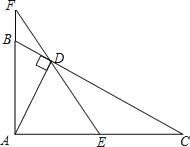
【题目】如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:
(1)△DFB∽△AFD;
(2)AB:AC=DF:AF.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)由已知条件得到∠BAC=∠ADB=![]() ,根据余角的性质得到∠BAD=∠C,由直角三角形的性质和对顶角相等得到∠BAD=∠BDF,即可得到结论;
,根据余角的性质得到∠BAD=∠C,由直角三角形的性质和对顶角相等得到∠BAD=∠BDF,即可得到结论;
(2)根据已知条件推出△ABD∽△CAD;于是得到![]() 由于△DFB∽△AFD;于是得到
由于△DFB∽△AFD;于是得到![]()
等量代换即可得到结论.
试题解析:(1)∵∠BAC=![]() ,AD⊥BC于D,
,AD⊥BC于D,
∴∠BAC=∠ADB=![]() ,
,
∴∠BAD+∠ABD=∠ABD+∠C=![]() ,
,
∴∠BAD=∠C,
∵E是AC的中点,
∴DE=CE,
∴∠C=∠EDC,
∵∠EDC=∠BDF,
∴∠BAD=∠BDF,
∵∠F=∠F,
∴△DFB∽△AFD;
(2)∵AD⊥BC,
∴∠ADB=∠ADC=![]() ,
,
∴∠BAD+∠DAC=![]() ,∠DAC+∠ACD=
,∠DAC+∠ACD=![]() ,
,
∴∠BAD=∠ACD,
∵∠ADB=∠ADC,
∴△ABD∽△CAD;
∴![]()
∵△DFB∽△AFD;
∴![]()
∴AB:AC=DF:AF.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
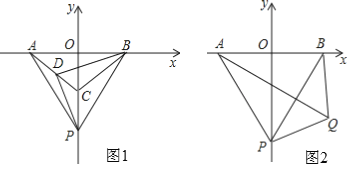
【题目】已知:如图1,在平面直角坐标系中,点A,B,C都在坐标轴上,且OA=OB=OC,△ABC的面积为9,点P从C点出发沿y轴负方向以1个单位/秒的速度向下运动,连接PA,PB,D(﹣m,﹣m)为AC上的点(m>0)
(1)试分别求出A,B,C三点的坐标;
(2)设点P运动的时间为t秒,问:当t为何值时,DP与DB垂直且相等?请说明理由;
(3)如图2,若PA=AB,在第四象限内有一动点Q,连QA,QB,QP,且∠PQA=60°,当Q在第四象限内运动时,求∠APQ与∠PBQ的度数和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 的解析式为
的解析式为![]() ,该直线与
,该直线与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,以
,以![]() 为边在第一象限内作正△ABC.若点
为边在第一象限内作正△ABC.若点![]() 在第一象限内,且满足
在第一象限内,且满足![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“节能减排,做环保小卫士”活动中,小明对两种照明灯的使用情况进行了调查,得出如表所示的数据:
功率 | 使用寿命 | 价格 | |
普通白炽灯 |
|
|
|
优质节能灯 |
|
|
|
已知这两种灯的照明效果一样,小明家所在地的电价是每度![]() 元.(注:用电度数
元.(注:用电度数![]() 功率(千瓦)
功率(千瓦)![]() 时间(小时),费用
时间(小时),费用![]() 灯的售价
灯的售价![]() 电费);如:若选用一盏普通白炽灯照明
电费);如:若选用一盏普通白炽灯照明![]() 小时,那么它的费用为
小时,那么它的费用为![]() (元),请解决以下问题:
(元),请解决以下问题:
(1)在白炽灯的使用寿命内,设照明时间为![]() 小时,请用含
小时,请用含![]() 的代数式分别表示用一盏白炽灯的费用
的代数式分别表示用一盏白炽灯的费用![]() ,(元)和一盏节能灯的费用
,(元)和一盏节能灯的费用![]() (元);
(元);
(2)在白炽灯的使用寿命内,照明多少小时时,使用这两种灯的费用相等?
(3)如果计划照明![]() 小时,购买哪一种灯更省钱?请你通过计算说明理由.
小时,购买哪一种灯更省钱?请你通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某包子铺每天供应黑猪鲜肉包、香菇青菜包、桂花豆沙包和其他特色包子.某一天,该包子铺共卖出包子6000个,且各类包子的销售情况如图所示,则下列说法正确的是( )
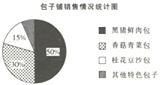
A.当天共卖出黑猪鲜肉包2000个B.当天香菇青菜包的销量是桂花豆沙包的3倍
C.当天其他特色包子在统计图中所对应的圆心角是![]() D.据此可以得出最受市民欢迎的包子是黑猪鲜肉包
D.据此可以得出最受市民欢迎的包子是黑猪鲜肉包
查看答案和解析>>
科目:初中数学 来源: 题型:
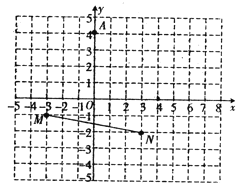
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(0,4),线段
的坐标为(0,4),线段![]() 的位置如图所示,其中点
的位置如图所示,其中点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(3,
的坐标为(3,![]() ).
).
(1)将线段![]() 平移得到线段
平移得到线段![]() ,其中点
,其中点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①点![]() 平移到点
平移到点![]() 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点![]() 的坐标为 .
的坐标为 .
(2)在(1)的条件下,若点![]() 的坐标为(4,0),连接
的坐标为(4,0),连接![]() ,画出图形并求
,画出图形并求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
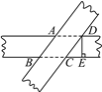
【题目】如图所示,将两条宽度相同的纸条交叉重叠放在一起,则重叠部分ABCD是________形,若纸条宽DE=4 cm,CE=3 cm,则四边形ABCD的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
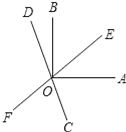
【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面上点![]() ,
,![]() ,
,![]() ,
,![]() (每三点都不在一条直线上).
(每三点都不在一条直线上).
(1)经过这四点最多能确定 条直线.
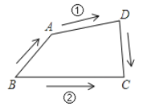
(2)如图这四点表示公园四个地方,如果点![]() ,
,![]() 在公园里湖对岸两处,
在公园里湖对岸两处,![]() ,
,![]() 在湖面上,要从
在湖面上,要从![]() 到
到![]() 筑桥,从节省材料的角度考虑,应选择图中两条路中的哪一条?如果有人想在桥上较长时间观赏湖面风光,应选择哪一条?为什么?
筑桥,从节省材料的角度考虑,应选择图中两条路中的哪一条?如果有人想在桥上较长时间观赏湖面风光,应选择哪一条?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com