
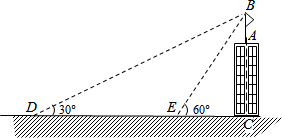
 如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41.
如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41. 分析 首先根据三角形外角的性质可得∠DBE=60°-30°=30°,根据等角对等边可得BE=DE,然后在Rt△BEC中,根据三角形函数可得BC=BE•sin60°,进而可得BC长,然后可得AB的长.
解答 解:∵∠BEC=60°,∠BDE=30°,
∴∠DBE=60°-30°=30°,
∴BE=DE=20,
在Rt△BEC中,
BC=BE•sin60°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$≈17.3(米),
∴AB=BC-AC=17.3-12=5.3(米),
答:旗杆AB的高度为5.3米.
点评 此题主要考查了解直角三角形的应用,关键是证明BE=DE,掌握三角形函数定义.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
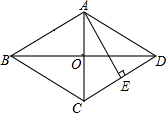 如图,在菱形ABCD中,AC与BD于点O,AE⊥CD,且AE=OD,若AO+OD+AD=3+$\sqrt{3}$,则菱形ABCD的面积是2$\sqrt{3}$.
如图,在菱形ABCD中,AC与BD于点O,AE⊥CD,且AE=OD,若AO+OD+AD=3+$\sqrt{3}$,则菱形ABCD的面积是2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
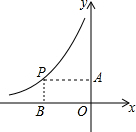 如图,点P是反比例函数$y=\frac{k}{x}$(x<0)图象的一点,PA垂直于y轴,垂足为点A,PB垂直于x轴,垂足为点B.若矩形PBOA的面积为6,则k的值为-6.
如图,点P是反比例函数$y=\frac{k}{x}$(x<0)图象的一点,PA垂直于y轴,垂足为点A,PB垂直于x轴,垂足为点B.若矩形PBOA的面积为6,则k的值为-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象在第一、三象限 | B. | 图象经过点(2,-8) | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 当x<0时,y随x的增大而增大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com