
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

【答案】![]()
【解析】
过点D作DE⊥DP交BC的延长线于E,先判断出四边形DPBE是矩形,再根据等角的余角相等求出∠ADP=∠CDE,再利用“角角边”证明△ADP和△CDE全等,根据全等三角形对应边相等可得DE=DP,然后判断出四边形DPBE是正方形,再根据正方形的面积公式解答即可.
解:如图,过点D作DE⊥DP交BC的延长线于E,

∵∠ADC=∠ABC=90°,
∴四边形DPBE是矩形,
∵∠CDE+∠CDP=90°,∠ADC=90°,
∴∠ADP+∠CDP=90°,
∴∠ADP=∠CDE,
∵DP⊥AB,
∴∠APD=90°,
∴∠APD=∠E=90°,
在△ADP和△CDE中,
∠ADP=∠CDE,∠APD=∠E,AD=CD,
∴△ADP≌△CDE(AAS),
∴DE=DP,四边形ABCD的面积=四边形DPBE的面积=18,
∴矩形DPBE是正方形,
∴DP=![]() .
.
故答案为:3![]() .
.
“点睛”本题考查了正方形的判定与性质,全等三角形的判定与性质,熟记各性质并作辅助线构造出全等三角形和正方形是解题的关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
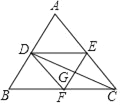
【题目】如图,△ABC中,∠ACB的平分线交AB于点D,作CD的垂直平分线,分别交AC、DC、BC于点E、G、F,连接DE、DF.
(1)求证:四边形DFCE是菱形;
(2)若∠ABC=60,∠ACB=45°,BD=2,试求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从超市出发,向东走了3千米到达小彬家,继续向东走了1.5千米到达小颖家,然后向西走了9.5千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,请你在数轴上表示出小明家、小彬家和小颖家的位置.
![]()
(2)小明家距小彬家多远?
(3)如果货车耗油量是每千米0.25升,那么在上述过程中共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
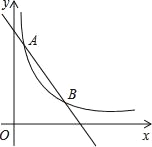
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ∥
∥![]() ,∠
,∠![]() =90°,
=90°,![]() =28cm,
=28cm, ![]() =24cm,
=24cm, ![]() =4cm,点
=4cm,点![]() 从点
从点![]() 出发,以1cm/s的速度向点
出发,以1cm/s的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 同时出发,以2cm/s的速度向点
同时出发,以2cm/s的速度向点![]() 运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动。则四边
运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动。则四边![]() 的面积
的面积![]() (cm2)与两动点运动的时间
(cm2)与两动点运动的时间![]() (s)的函数图象大致是( )
(s)的函数图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为xA=﹣5和xB=6,动点P从点A出发,以每秒1个单位的速度沿数轴在A,B之间往返运动,同时动点Q从点B出发,以每秒2个单位的速度沿数轴在B,A之间往返运动.设运动时间为t秒.
(1)当t=2时,点P对应的有理数xP=______,PQ=______;
(2)当0<t≤11时,若原点O恰好是线段PQ的中点,求t的值;
(3)我们把数轴上的整数对应的点称为“整点”,当P,Q两点第一次在整点处重合时,直接写出此整点对应的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a,b分别是数轴上两个不同的点A,B所表示的有理数,且![]() =5,
=5,![]() =2,A,B两点在数轴上的位置如图所示:
=2,A,B两点在数轴上的位置如图所示:
![]()
(1) 试确定数a,b;
(2) A,B两点相距多少个单位长度?
(3)若C点在数轴上,C点B点的距离是C点到A点距离的![]() ,求C点表示的数;
,求C点表示的数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应点之间的距离.这个结论可以推广为:
对应点之间的距离.这个结论可以推广为:![]() 表示在数轴上数
表示在数轴上数![]() 与
与![]() 对应点之间的距离.
对应点之间的距离.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与![]() 的距离为
的距离为![]() 点的对应数为
点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
仿照阅读材料的解法,解决下列问题:
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)若数轴上表示![]() 的点在
的点在![]() 与
与![]() 之间,则
之间,则![]() 的值为_________;
的值为_________;
(4)当![]() 满足_________时,则
满足_________时,则![]() 的值最小,最小值是_________.
的值最小,最小值是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com