
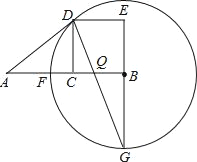
【题目】设C为线段AB的中点,四边形BCDE是以BC为一边的正方形.以B为圆心,BD长为半径的⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
求证:(1)AD是⊙B的切线;(2)AD=AQ;(3)BC2=CFEG.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】试题分析:(1)连接BD,由DC⊥AB,C为AB的中点,由线段垂直平分线的性质,可得AD=BD,再根据正方形的性质,可得∠ADB=90°;
(2)由BD=BG与CD∥BE,利用等边对等角与平行线的性质,即可求得∠G=∠CDG=∠BDG=![]() ∠BCD=22.5°,继而求得∠ADQ=∠AQD=67.5°,由等角对等边,可证得AD=AQ;
∠BCD=22.5°,继而求得∠ADQ=∠AQD=67.5°,由等角对等边,可证得AD=AQ;
(3)易求得∠GDE=∠GDB+∠BDE=67.5°=∠DFE,∠DCF=∠E=90°,即可证得Rt△DCF∽Rt△GED,根据相似三角形的对应边成比例,即可证得结论.
试题解析:
(1)连接BD,
∵四边形BCDE是正方形,
∴∠DBA=45°,∠DCB=90°,即DC⊥AB,
∵C为AB的中点,
∴CD是线段AB的垂直平分线,
∴AD=BD,
∴∠DAB=∠DBA=45°,
∴∠ADB=90°,
即BD⊥AD,
∵BD为半径,
∴AD是⊙B的切线;
(2)∵BD=BG,
∴∠BDG=∠G,
∵CD∥BE,
∴∠CDG=∠G,
∴∠G=∠CDG=∠BDG=![]() ∠BCD=22.5°,
∠BCD=22.5°,
∴∠ADQ=90°﹣∠BDG=67.5°,∠AQB=∠BQG=90°﹣∠G=67.5°,
∴∠ADQ=∠AQD,
∴AD=AQ;
(3)连接DF,
在△BDF中,BD=BF,
∴∠BFD=∠BDF,
又∵∠DBF=45°,
∴∠BFD=∠BDF=67.5°,
∵∠GDB=22.5°,
在Rt△DEF与Rt△GCD中,
∵∠GDE=∠GDB+∠BDE=67.5°=∠DFE,∠DCF=∠E=90°,
∴Rt△DCF∽Rt△GED,
∴![]() ,
,
又∵CD=DE=BC,
∴BC2=CFEG.



 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示从上到下第m排,从左到右第n个数,如(4,2)表示整数8.则(62,55)表示的数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北海市创建全国文明城活动中,需要30名志愿者担任“讲文明树新风”公益广告宣传工作,其中男生18人,女生12人.
(1)若从这30人中随机选取一人作为“展板挂图”讲解员,求选到女生的概率;
(2)若“广告策划”只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲担任,否则乙担任.试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李对初三(1)班全体同学的业余兴趣爱好(第一爱好)进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.

请你根据图中提供的信息,解答下列问题:
(1)初三(1)班共有学生________人;
(2)在图1中,将“书画”部分的图形补充完整;
(3)在图2中,“球类”部分所对应的圆心角的度数________度;爱好“音乐”的人数占本班学生数的百分数是________;爱好“书画”的人数占本班学生数的百分数是________;“其它”的人数占本班学生数的百分数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明学习了《有理数》后,对运算非常感兴趣,于是定义了一种新运算“△”规则如下:对于两个有理数m , n , m △ n =![]() .
.
(1)计算:1△(-2)= ;
(2)判断这种新运算是否具有交换律,并说明理由;
(3)若a![]() =| x-1| , a
=| x-1| , a![]() =| x-2|,求a
=| x-2|,求a![]() △ a
△ a ![]() (用含 x 的式子表示)
(用含 x 的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列视图问题:
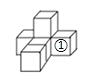
(1)如图(1),它是由6个同样大小的正方体摆成的几何体,将正方体①移走后,新几何体从三个方向看到的图形与原几何体从三个方向看到的图形相比,从 方向看到的形状图没有发生改变?
(2)如图(2),请你在右侧虚线网格图a中画出该几何体从上面看到的形状图
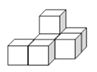
(3)如图(3),它是由几个小立方块组成从上面看到的形状图,小正方形上的数字表示该位置上的正方体的个数,请你在右侧建线网格图b中面出该几何体从正面看到的形状图.
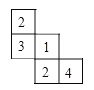
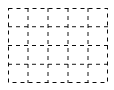
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗洪抢险中,人民解放军的冲锋舟沿东西方向的河流抢救灾民,早晨从![]() 地出发,晚上最后到达
地出发,晚上最后到达![]() 地,约定向东为正方向,当天航行依次记录如下(单位:千米)
地,约定向东为正方向,当天航行依次记录如下(单位:千米)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,问:
,问:
(1)![]() 地在
地在![]() 地的东面,还是西面?与
地的东面,还是西面?与![]() 地相距多少千米?
地相距多少千米?
(2)这一天冲锋舟离![]() 最远多少千米?
最远多少千米?
(3)若冲锋舟每千米耗油![]() 升,邮箱容量为
升,邮箱容量为![]() 升,求途中至少需要补充多少升油?
升,求途中至少需要补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点,连接
上一点,连接![]() 交对角线
交对角线![]() 于点
于点![]() .
.
(1)如图1,已知![]() 于
于![]() ,菱形的边长为6,求线段
,菱形的边长为6,求线段![]() 的长度;
的长度;
(2)如图2,已知点![]() 为边
为边![]() 上一点,连接
上一点,连接![]() 交线段
交线段![]() 于点
于点![]() ,且满足
,且满足![]() ,
,![]() ,求证:
,求证:![]() .
.
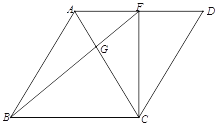
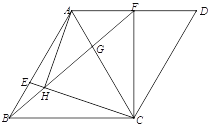
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为: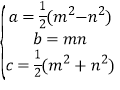 其中m>n>0,m,n是互质的奇数.
其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com