
【题目】(1)(学习心得)
于彤同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.

例如:如图1,在△ABC中,AB=AC,∠BAC=90°,D是△ABC外一点,且AD=AC,求∠BDC的度数.若以点A为圆心,AB为半径作辅助⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC是圆周角,从而可容易得到∠BDC= °.
(2)(问题解决)
如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=25°,求∠BAC的度数.
(3)(问题拓展)
如图3,如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
【答案】(1)45;(2)∠BAC=25°;(3)![]() ﹣1
﹣1
【解析】
(1)利用同弦所对的圆周角是所对圆心角的一半求解.
(2)由A、B、C、D共圆,得出∠BDC=∠BAC,
(3)根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边”证明△ABE和△DCF全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△ADG和△CDG全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AHB=90°,取AB的中点O,连接OH、OD,根据直角三角形斜边上的中线等于斜边的一半可得OH=![]() AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.
AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.
解:(1)如图1,
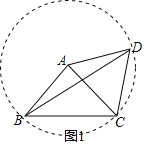
∵AB=AC,AD=AC,
∴以点A为圆心,点B、C、D必在⊙A上,
∵∠BAC是⊙A的圆心角,而∠BDC是圆周角,
∴∠BDC=![]() ∠BAC=45°,
∠BAC=45°,
故答案是:45;
(2)如图2,取BD的中点O,连接AO、CO.

∵∠BAD=∠BCD=90°,
∴点A、B、C、D共圆,
∴∠BDC=∠BAC,
∵∠BDC=25°,
∴∠BAC=25°,
(3)如图3,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,

 ,
,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,
 ,
,
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°﹣90°=90°,
取AB的中点O,连接OH、OD,
则OH=AO=![]() AB=1,
AB=1,
在Rt△AOD中,OD=![]() ,
,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
最小值=OD﹣OH=![]() ﹣1.
﹣1.
故答案为:![]() ﹣1.
﹣1.


科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4张卡片,卡片上分別标有数字1、﹣2、3、﹣4,这些卡片除数字外都相同.王兴从口袋中随机抽取一张卡片,钟华从剩余的三张卡片中随机抽取一张,求两张卡片上数字之积.
(1)请你用画树状图或列表的方法,列出两人抽到的数字之积所有可能的结果.
(2)求两人抽到的数字之积为正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中抛物线y=(x+1)(x﹣3)与x轴相交于A、B两点,若在抛物线上有且只有三个不同的点C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面积都等于m,则m的值是( )
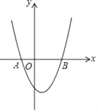
A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,两条平行的高速公路AB和CD之间有一条“L”型道路连通,“L”型道路中的EP=FP=20千米,∠BEP=12°,∠EPF=80°,求AB和CD之间的距离.(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)-(3)题.
数学课上,老师出示了这样一道题:
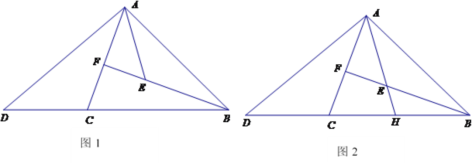
如图1,在△ABC中,BA=BC,![]() .点F在AC上,点E在BF上,
.点F在AC上,点E在BF上,![]() .点D在BC 延长线上,连接AD、AE,∠ACD+∠DAE=180゜.探究线段AD与AE的数量关系并证明.
.点D在BC 延长线上,连接AD、AE,∠ACD+∠DAE=180゜.探究线段AD与AE的数量关系并证明.
同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现∠CAD与∠EAB相等.”
小亮:“通过观察和度量,发现∠FAE与∠D也相等.”
小伟:“通过边角关系构造辅助线,经过进一步推理,可以得到线段AD与AE的数量关系.”
![]()
老师:“保留原题条件,延长图1中的AE,与BC相交于点H(如图2),若知道DH与AH的数量关系,可以求出![]() 的值.”
的值.”
(1)求证:∠CAD=∠EAB;
(2)求![]() 的值(用含k的式子表示);
的值(用含k的式子表示);
(3)如图2,若![]() ,则
,则![]() 的值为________(用含k的式子表示).
的值为________(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区2014年八年级学生的体育测试情况,随机抽取了该区若干名八年级学生的测试成绩进行了统计分析,并根据抽取的成绩等级绘制了如下的统计图表![]() :
:
成绩等级 | A | B | C | D |
人数 | 60 | 10 |
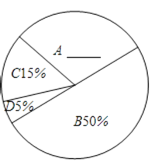

请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有______ 名,成绩为B类的学生人数为______ 名,C类成绩所在扇形的圆心角度数为______
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该区约5000名八年级学生体育测试成绩为D类的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
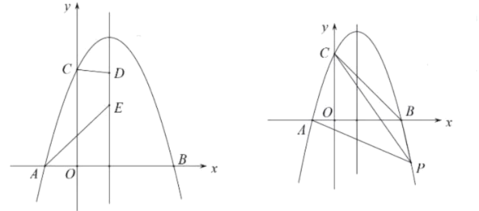
【题目】如图所示抛物线![]() 过点
过点![]() ,点
,点![]() ,且
,且![]()
(1)求抛物线的解析式及其对称轴;
(2)点![]() 在直线
在直线![]() 上的两个动点,且
上的两个动点,且![]() ,点
,点![]() 在点
在点![]() 的上方,求四边形
的上方,求四边形![]() 的周长的最小值;
的周长的最小值;
(3)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为3∶5两部分,求点
的面积分为3∶5两部分,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为的网格中,点![]() 均在格点上,
均在格点上,![]() 为小正方形边中点.
为小正方形边中点.
(1)![]() 的长等于 ______;
的长等于 ______;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个点![]() ,使其满足
,使其满足![]() 说明点
说明点![]() 的位置是如何找到的(不要求证明)______.
的位置是如何找到的(不要求证明)______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com