
����Ŀ����֪����ͼ��OΪ����ԭ�����ı���OABCΪ������A��10��0����C��0��4������D��OA�е�����P��BC����ÿ��1����λ���ٶ���C��B�˶������˶�ʱ��Ϊt�룮

��1����ODP�����S=________��
��2��tΪ��ֵʱ���ı���PODB��ƽ���ı��Σ�
��3�����߶�PB���Ƿ����һ��Q��ʹ��ODQPΪ���Σ�����������t��ֵ�������Q���������������������˵��������
��4������OPDΪ��������������д���������������ĵ�P�����꣨��ֱ��д����������д���̣�
���𰸡���1��10����2��5����3����8��4������4�����������ĵ�P������ΪP1��3��4����P2��2.5��4����P3��2��4����P4��8��4��.
��������
������1�����������ε������ʽ���������ODP�����S��
��2������PB��OD������ƽ���ı��ε��ж���֪��PB=OD=5ʱ���ı���PODB��ƽ���ı��Σ������PC=5���Ӷ����t��ֵ��
��3���������ε��ж�����OD=OP=PQ=5ʱ���ı���ODQPΪ���Σ���Rt��OPC�У����ù��ɶ������CP��ֵ���������t��ֵ��Q������ꣻ
��4������OPDΪ����������ʱ������������������ۣ������OΪ���㣬��ôOP=OD=5�������PΪ���㣬��ôPO=PD�������DΪ���㣬��ôDP=DO=5���ֱ��������ߣ����ù��ɶ������P�������.
�����������1����OΪ����ԭ�㣬A��10��0�����ı���OABCΪ���Σ�C��0��4����
��OA=BC=10��OC=4��
����D��OA�е㣬
��OD=DA= ![]() OA=5��
OA=5��
���ODP�����S= ![]() ODOC=
ODOC= ![]() ��5��4=10��
��5��4=10��
��2���⣺��PB��OD��
�൱PB=ODʱ���ı���PODB��ƽ���ı��Σ�
��OD=5��
��PB=5��
��PC=BC��PB=10��5=5��
�ߵ�P��BC����ÿ��1����λ���ٶ���C��B�˶���
��t=5
��3���⣺��OD=OP=PQ=5ʱ��ODQPΪ���Σ�
��Rt��OPC�У��ɹ��ɶ����ã�
PC= ![]() =
= ![]() =3��
=3��
��t=3��CQ=CP+PQ=3+5=8��
��Q���������8��4��
��4���⣺��OPDΪ����������ʱ�������������
�����OΪ���㣬��ôOP=OD=5��
�ɹ��ɶ����������PC=3����ʱP1��3��4����
�����PΪ���㣬��ôPO=PD��
��PE��OA��E����OE=ED=2.5����ʱP2��2.5��4����
�����DΪ���㣬��ôDP=DO=5��
��DF��BC��F���ɹ��ɶ�������PF=3��
��P3C=5��3=2��P4C=5+3=8����ʱP3��2��4����P4��8��4����
�������������������ĵ�P������ΪP1��3��4����P2��2.5��4����P3��2��4����P4��8��4����




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ճ������У���ȡ������ȶ���Ҫ���룮��һ��������ʽ�ֽ��������������룬������䣮ԭ���ǣ�����ڶ���ʽx4��y4����ʽ�ֽ�Ľ����(x��y)(x��y)��(x2��y2)����ȡx��9��y��9ʱ���������ʽ��ֵ�ǣ�(x��y)��0��(x��y)��18��x2��y2��162�����ǾͿ�����018162����Ϊһ����λ�������룮���ڶ���ʽ4x3��xy2��ȡx��10��y��10ʱ���������������������빲�ж����֣�����ֱ�д������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽����еĿ������������ij������ȤС��ӻ�������������ȡ��������Ŀ������������Ϊ��������ͳ�ƣ���������ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��������Ϣδ�������� 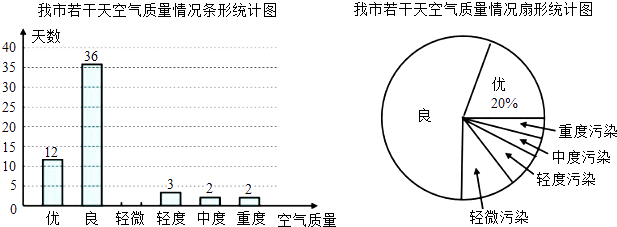
�������ͼ���ṩ����Ϣ������������⣺
��1�����㱻��ȡ��������
��2���벹ȫ����ͳ��ͼ����������ͳ��ͼ�б�ʾ���š������ε�Բ�ĽǶ�����
��3������Ƹ�����һ�꣨365�죩�ﵽ���š��͡���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ���E��K�ֱ��ڱ�BC��AB�ϣ���G��BA���ӳ����ϣ���CE=BK=AG.
��1����֤����DE=DG�� ��DE��DG��
��2���߹���ͼ�����߶�DE��DGΪ������������DEFG��Ҫ��ֻ������ͼ�ۼ�����д������֤������
��3�����ӣ�2���е�KF�����벢д���ı���CEFK�������������ı��Σ���֤����IJ��룻
��4����![]() =
=![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() ��ֵ.
��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�գ������ҹ��Ϻ�������ҵ��һ�Ҵ����洬ͻȻ�������飬��ز��Žӵ�����źź�������Dzһ��ֱ���ɻ���һ�������Ϻ�Ѳ����������ǰ����Ԯ�����ɻ����ﺣ��3000m�ĸ߿�C��ʱ�����A���������ĸ���Ϊ45�㣬���B�����������洬�ĸ���Ϊ30�㣬��ʱ���������洬�ľ���AB�ǣ� �� 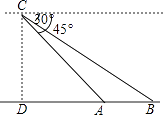
A.3000 ![]() m
m
B.3000�� ![]() +1��m
+1��m
C.3000�� ![]() -1��m
-1��m
D.1500 ![]() m
m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1�����㣺����1��2016��4cos60��+�� ![]() ��0����
��0���� ![]() ����2��
����2��
��2���Ȼ�������ֵ�� ![]() ������3x+6y��1=0��
������3x+6y��1=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ��˾����Ƴ�һ���ζ���̣����к��桢ľ�����ֿ�ζ��������Ա�������죬ÿ�������ѡһƿij�ֿ�ζ����������ijס��Ʒ�������ס���յ�����ƿ�����У���������ƿΪ�����ζ�ĸ����Ƕ��٣�
�����á�����״ͼ���ķ��������������̣�����������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com