
如图,AD=BC,AC=BD,AC、BD相交于O,求证:AB∥CD.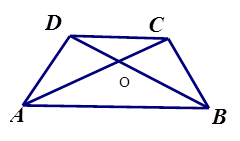
证出 △ABD≌△BAC , 证出AB∥CD
解析考点:全等三角形的判定与性质。
分析:
(1)根据题意,结合“sss”判定定理,即可推出△ABD≌△BAC、△DCA≌△CDB,
(2)由△ABD≌△BAC,即可推出AB∥CD。
解答:
在图中:四边形ABCD中,AD=BC,AC=BD,AC与BD相交于O点,
由“SSS”可判定△ABD≌△BAC、△DCA≌△CDB这二对三角形全等。
理由是AD=BC,AC=BD,公共边AB,则△ABD≌△BAC。
同理AD=BC,AC=BD,公共边DC,则△DCA≌△CDB。
∵△ABD≌△BAC
∴∠ABD=∠BAC;
∵△DCA≌△CDB,
∴∠DCA=∠CDB。
又∠AOB=∠DOC(对顶角相等)
∴∠ABD=∠CDB
∴AB∥CD(内错角相等两直线平行)。
点评:本题主要考查全等三角形的判定和性质,关键在于根据判定定理求证相关三角形全等。


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com